题目内容
3. 如图,在四边形ABCD中,AB∥CD,AD⊥DC,AB=BC,点E为BC上一点,且CD=CE.
如图,在四边形ABCD中,AB∥CD,AD⊥DC,AB=BC,点E为BC上一点,且CD=CE.(1)求证:AE⊥BC;
(2)若AD=6,DC=3,求AB的长.
分析 (1)连接AC,求出∠DCA=∠ECA,根据SAS推出△DCA≌△ECA,根据全等得出∠D=∠CEA,即可得出答案;
(2)根据全等得出AE=AD=6,设AB=x,根据勾股定理得出方程,求出方程的解即可.
解答 (1)证明: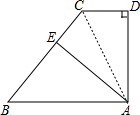
连接AC,
∵AB=BC,
∴∠ECA=∠BAC,
∵AB∥CD,
∴∠DCA=∠BAC,
∴∠DCA=∠ECA,
在△DCA和△ECA中
$\left\{\begin{array}{l}{CA=CA}\\{∠DCA=∠ECA}\\{DC=EC}\end{array}\right.$
∴△DCA≌△ECA(SAS),
∴∠D=∠CEA,
∵AD⊥DC,
∴∠D=90°,
∴∠CEA=90°,
∴AE⊥BC;
(2)解:∵△DCA≌△ECA,
∴AE=AD=6,
设AB=x,
∵DC=CE=3,
∴在Rt△BEA中,由勾股定理得:AB2=BE2+AE2,
∵AB=BC,
∴x2=(x-3)2+62,
解得:x=7.5,
即AB=7.5.
点评 本题考查了等腰三角形的性质,全等三角形的性质和判定,勾股定理的应用,能推出△DCA≌△ECA是解此题的关键.

练习册系列答案
相关题目
12.方程x2+2x=0的解是( )
| A. | x1=0,x2=2 | B. | x1=0,x2=-2 | C. | x=2 | D. | x=-2 |
13.下列各组中的两项不是同类项的是( )
| A. | -25mm和3mn | B. | 7.2a2b和$\frac{1}{4}$a2c | C. | x2y2与-3y2x2 | D. | -125和93 |
 如图,AB+AC> BC(填“>”,“<”或“=”),理论依据是三角形两边之和大于第三边.
如图,AB+AC> BC(填“>”,“<”或“=”),理论依据是三角形两边之和大于第三边. 一辆货车从甲地匀速驶往乙地用了2.7小时,到达后用了0.5小时卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍,货车离甲地的距离y(千米)关于时间x(小时)的函数图象如图所示,则a=5(小时).
一辆货车从甲地匀速驶往乙地用了2.7小时,到达后用了0.5小时卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍,货车离甲地的距离y(千米)关于时间x(小时)的函数图象如图所示,则a=5(小时). 已知如图,AB=10,点C为线段AB上一点,点D、E分别为线段AB、AC的中点,ED=1,求线段AC的长.
已知如图,AB=10,点C为线段AB上一点,点D、E分别为线段AB、AC的中点,ED=1,求线段AC的长. 如图,一次函数y=x+3的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,AB=4$\sqrt{2}$,则k=$\frac{7}{4}$.
如图,一次函数y=x+3的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A,B两点,AB=4$\sqrt{2}$,则k=$\frac{7}{4}$.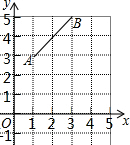 如图,在平面直角坐标系中,把线段AB先向右平移2个单位,再向下平移3个单位,得到线段CD,请画出线段CD并分别写出点A、B、C、D的坐标.
如图,在平面直角坐标系中,把线段AB先向右平移2个单位,再向下平移3个单位,得到线段CD,请画出线段CD并分别写出点A、B、C、D的坐标.