题目内容
 如图所示,已知菱形ABCD中,E、F分别在BC和CD上,且∠B=∠EAF=60°,∠BAE=15°,求∠CEF的度数.
如图所示,已知菱形ABCD中,E、F分别在BC和CD上,且∠B=∠EAF=60°,∠BAE=15°,求∠CEF的度数.考点:菱形的性质,全等三角形的判定与性质
专题:
分析:根据菱形的四条边都相等可得AB=BC,然后求出△ABC是等边三角形,根据等边三角形的性质可得AB=AC,∠BAC=60°,再求出∠BAE=∠CAF,∠B=∠ACD,然后利用“角边角”证明△ABE和△ACF全等,根据全等三角形对应边相等可得AE=AF,再求出△AEF是等边三角形,根据等边三角形的性质可得∠AEF=60°,再利用三角形的一个外角等于与它不相邻的两个内角的和可得∠AEF+∠CEF=∠B+∠BAE,从而得到∠CEF=∠BAE.
解答:解:如图,在菱形ABCD中,AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵AB∥CD,
∴∠ACD=∠BAC=60°,
∴∠B=∠ACD=60°,
又∵∠EAF=60°,
∴∠BAE=∠CAF,
在△ABE和△ACF中,
,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形,
∴∠AEF=60°,
∵由三角形的外角性质,∠AEF+∠CEF=∠B+∠BAE,
∴∠CEF=∠BAE=15°.
∵∠B=60°,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵AB∥CD,
∴∠ACD=∠BAC=60°,
∴∠B=∠ACD=60°,
又∵∠EAF=60°,
∴∠BAE=∠CAF,
在△ABE和△ACF中,
|
∴△ABE≌△ACF(ASA),
∴AE=AF,
∵∠EAF=60°,
∴△AEF是等边三角形,
∴∠AEF=60°,
∵由三角形的外角性质,∠AEF+∠CEF=∠B+∠BAE,
∴∠CEF=∠BAE=15°.
点评:本题考查了菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质,熟记性质并作辅助线构造出全等三角形和等边三角形是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在下列方程中,是二元一次方程的是( )
| A、x-3x=0 |
| B、5x-2y=0 |
| C、x+y=z |
| D、x-2(x-1)=0 |
已知x>y,则下列不等式不成立的是( )
| A、x-6>y-6 |
| B、2x>2y |
| C、-3x<-3y |
| D、-3x+6>-3y+6 |
 在边长为2的正方形ABCD的边BC上,有一点P由B点向C点方向运动(P与C不重合),设PB=x,四边形APCD的面积为y,
在边长为2的正方形ABCD的边BC上,有一点P由B点向C点方向运动(P与C不重合),设PB=x,四边形APCD的面积为y,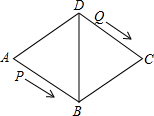 如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB-BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动.
如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB-BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动.