题目内容
11. 如图,正三角形ABC内接于⊙O连接CD,AD是⊙O的内接正十二边形的一边.若CD=12,求圆O的半径.
如图,正三角形ABC内接于⊙O连接CD,AD是⊙O的内接正十二边形的一边.若CD=12,求圆O的半径.
分析 首先连接OA、OD、OC,由等边△ABC内接于⊙O,AD为内接正十二边形的一边,可求得∠AOC,∠AOD的度数,继而证得△COD是等腰直角三角形,继而求得答案.
解答 解:连接OA、OD、OC,如图所示: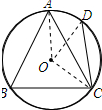
∵等边△ABC内接于⊙O,AD为内接正十二边形的一边,
∴∠AOC=$\frac{1}{3}$×360°=120°,∠AOD=$\frac{1}{12}$×360°=30°,
∴∠COD=∠AOC-∠BAD=90°,
∵OC=OD,
∴△OCD是等腰直角三角形,
∴OC=OD=$\frac{\sqrt{2}}{2}$CD=6$\sqrt{2}$,
即⊙O的半径为6$\sqrt{2}$.
点评 此题考查了正多边形与圆、等边三角形的性质、等腰直角三角形的判定与性质、勾股定理.此题难度适中,注意掌握辅助线的作法,证明三角形是等腰直角三角形是解题的关键.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 一水库大坝的横断面为梯形ABCD,坝顶宽6.2米,坝高23.5米,斜坡AB的坡度iAB=1:3,斜坡CD的坡角是21°,求:
一水库大坝的横断面为梯形ABCD,坝顶宽6.2米,坝高23.5米,斜坡AB的坡度iAB=1:3,斜坡CD的坡角是21°,求: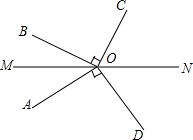 如图,已知∠AOB为锐角,∠AOD=∠BOC=90°,OM,ON分别是∠AOB和∠COD的平分线.
如图,已知∠AOB为锐角,∠AOD=∠BOC=90°,OM,ON分别是∠AOB和∠COD的平分线.