题目内容
19.已知关于x的一元二次方程(x-3)(x-2)=m2(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
分析 (1)先把方程(x-3)(x-2)=m2,变形为x2-5x+6-m2=0,得出△=25-4(6-m2)=1+4m2>0,即可得出答案;
(2)把1代入原方程,得出m,再把原方程变形为x2-6x+4=0,设方程的另一个根为a,根据根与系数的关系求出方程的另一个根即可.
解答 解:(1)∵关于x的一元二次方程(x-3)(x-2)=m2,
∴x2-5x+6-m2=0,
∴△=25-4(6-m2)=1+4m2>0,
∴对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,
则(1-3)×(1-2)=m2,
2=m2,
m=±$\sqrt{2}$,
原方程变形为x2-5x+4=0,
设方程的另一个根为a,
则1×a=4,
a=4,
则方程的另一个根为4.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac和一元二次方程的根与系数的关系:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
7.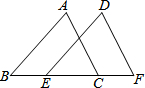 如图,△ABC和△DEF中,已知AB=DE,BC=EF,根据“SAS”判定△ABC≌△DEF还需要的条件是( )
如图,△ABC和△DEF中,已知AB=DE,BC=EF,根据“SAS”判定△ABC≌△DEF还需要的条件是( )
 如图,△ABC和△DEF中,已知AB=DE,BC=EF,根据“SAS”判定△ABC≌△DEF还需要的条件是( )
如图,△ABC和△DEF中,已知AB=DE,BC=EF,根据“SAS”判定△ABC≌△DEF还需要的条件是( )| A. | ∠A=∠D | B. | ∠B=∠DEF | C. | ∠ACB=∠F | D. | 以上均可以 |
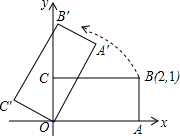 如图在平面直角坐标系中,矩形OABC的一顶点为坐标原点O,边OA、OC分别落在x轴和y轴上,点B的坐标为(2,1);矩形OA′B′C′是由矩形OABC旋转而来的,∠C′OA=150°.
如图在平面直角坐标系中,矩形OABC的一顶点为坐标原点O,边OA、OC分别落在x轴和y轴上,点B的坐标为(2,1);矩形OA′B′C′是由矩形OABC旋转而来的,∠C′OA=150°. 如图,正三角形ABC内接于⊙O连接CD,AD是⊙O的内接正十二边形的一边.若CD=12,求圆O的半径.
如图,正三角形ABC内接于⊙O连接CD,AD是⊙O的内接正十二边形的一边.若CD=12,求圆O的半径.