题目内容
14.在△ABC中∠A、∠C均为锐角,且有$|{tanB-\sqrt{3}}|+{({sinA-\frac{{\sqrt{3}}}{2}})^2}=0$,则△ABC的形状为等边三角形.分析 根据非负数的性质求出tanB和sinA的值,然后求出∠A、∠B的度数,即可判断△ABC的形状.
解答 解:由题意得,tanB=$\sqrt{3}$,sinA=$\frac{\sqrt{3}}{2}$,
则∠A=60°,∠B=60°,
∠C=180°-60°-60°=60°.
故△ABC为等边三角形.
故答案为:等边三角形.
点评 本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值以及非负数的性质.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
4.2010央视为青海玉树县举办的赈灾晚会共募得善款21.75亿元.把21.75亿元用科学记数法表示为( )
| A. | 2.175×108元 | B. | 2.175×107 元 | C. | 2.175×109 元 | D. | 2.175×106元 |
5.方程(x-4)2=81的解是( )
| A. | x=13 | B. | x=-5 | C. | x=13或-5 | D. | 以上都不对 |
9.下列命题中,真命题是( )
| A. | 有两边相等的平行四边形是菱形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 四个角相等的菱形是正方形 | D. | 两条对角线相等的四边形是矩形 |
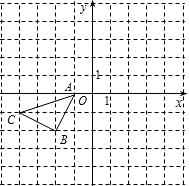 如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题: 作出△ABC关于点O的中心对称图形(保留痕迹).
作出△ABC关于点O的中心对称图形(保留痕迹).