题目内容
18.在平面直角坐标系中,A(-3,1),B($\frac{5}{3},\frac{17}{3}$),若抛物线y=x2+2mx+m2+$\frac{1}{3}$m与线段AB只有1个公共点,则m的取值范围是-$\frac{13}{3}$<m<$\frac{2}{3}$.分析 求得线段AB的解析式,然后联立方程求得x2+(2m-1)x+m2+$\frac{1}{3}$m-4=0,转化为函数与x轴的关系,令y′=x2+(2m-1)x+m2+$\frac{1}{3}$m-4,结合二次函数图象上点的坐标特征求解即可.
解答 解:根据题意:线段AB:y=x+4(-3≤x≤$\frac{5}{3}$),
与y=x2+2mx+m2+$\frac{1}{3}$m联立得:
x2+(2m-1)x+m2+$\frac{1}{3}$m-4=0,
令y′=x2+(2m-1)x+m2+$\frac{1}{3}$m-4,
若抛物线y=x2+(2m-1)x+m2+$\frac{1}{3}$m-4与线段AB只有1个公共点,
即函数y′在-3≤x≤$\frac{5}{3}$范围内只有一个零点
当x=-3时,y′=m2+$\frac{19}{3}$m+2<0,
∵△>0,
∴此种情况不存在,
当x=$\frac{5}{3}$时,y′=m2+$\frac{11}{3}$m-$\frac{26}{9}$<0,
解得-$\frac{13}{3}$<m<$\frac{2}{3}$
故答案为-$\frac{13}{3}$<m<$\frac{2}{3}$.
点评 本题考查了直线与抛物线的位置关系,考查了转化思想和数形结合的数学思想.

练习册系列答案
相关题目
6.把数-1,-2,-3,-4,-5,-6,-7,-8,-9分别填入图中的每个方格中,使得每行的3个数,每列的3个数,斜对角的3个数的和都相等.
通过填数,你发现怎样填入才能填得快?
| -8 | -1 | -6 |
| -3 | -5 | -7 |
| -4 | -9 | -2 |
7.下列等式由左到右的变形是因式分解的是( )
| A. | a2-b2+1=(a+b)(a-b)+1 | B. | xy(x2+y2)(x+y)(x-y)=x5y-xy5 | ||
| C. | (m+3)2=m2+9 | D. | x2-9=(x+3)(x-3) |
6.下列方程中是一元一次方程的是( )
| A. | xy=2 | B. | 2x2-x-1=0 | C. | x-2y=4 | D. | 3(2x-7)=4(x-5) |
 如图,⊙O的直径CB的延长线与弦ED的延长线交于点A,且$\widehat{CE}$=$\widehat{BE}$,∠A=20°,则∠C=25°.
如图,⊙O的直径CB的延长线与弦ED的延长线交于点A,且$\widehat{CE}$=$\widehat{BE}$,∠A=20°,则∠C=25°.
 如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过(1,0),B(0,-6)两点,
如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过(1,0),B(0,-6)两点,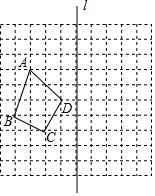 请你在所给的网格中画出四边形A'B'C'D',使四边形A'B'C'D'和四边形ABCD关于直线l对称.
请你在所给的网格中画出四边形A'B'C'D',使四边形A'B'C'D'和四边形ABCD关于直线l对称.