题目内容
3.解方程(1)x2-2x=0.
(2)用公式法解方程:2x2-4x-5=0.
(3)用配方法解方程:x2-4x+1=0.
(4)用因式分解法解方程:(y-1)2+2y(1-y)=0.
分析 (1)根据提公因式法分解因式即可;
(2)先找a,b,c,再求△,根据根的判别式判断方程根的情况,再代入公式计算即可;
(3)先移项,再方程两边同加上一次项系数一般半的平方,再直接开平方即可;
(4)先变形,再提公因式,得出两个一元一次方程求解即可.
解答 解:(1)提公因式得,x(x-2)=0,
∴x1=0,x2=2.
(2)∵a=2,b=-4,c=-5,
∴b2-4ac=(-4)2-4×2×(-5)=56>0.
∴x=$\frac{4±\sqrt{56}}{2×2}$=$\frac{4±2\sqrt{14}}{4}$.
∴x1=$\frac{2+\sqrt{14}}{2}$,x2=$\frac{2-\sqrt{14}}{2}$.
(3)∵x2-4x+1=0,
∴x2-4x+4=4-1,即(x-2)2=3.
∴x1=2+$\sqrt{3}$,x2=2-$\sqrt{3}$.
(4)∵(y-1)2+2y(1-y)=0,
∴(y-1)2-2y(y-1)=0.
∴(y-1)(y-1-2y)=0.
∴y-1=0或y-1-2y=0.
∴y1=1,y2=-1.
点评 本题考查了一元二次方程的解法,一元二次方程的解法,有配方法,公式法以及因式分解法.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
13.已知ab>0,a>0,ac>0,下列结论判断正确的是( )
| A. | b<0,c<0 | B. | b>0,c<0 | C. | b<0,c<0 | D. | b>0,c>0 |
14.若函数y=x2的图象经过A(a-1,y1)、B(a,y2)、c(a+1,y3)三点,且a<-1,则( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y3 | D. | y2<y1<y3 |
15. 如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )
如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )
 如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )
如图所示,点D在△ABC外部,点E在BC边上,DE交AC于F,若∠1=∠2,∠D=∠C,AE=AB,则( )| A. | △ABC≌△AFE | B. | △AFE≌△ADC | C. | △AFE≌△DFC | D. | △ABC≌△AED |
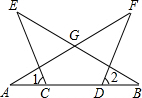 如图,已知:CE=DF,AC=BD,∠1=∠2.求证:△GAB是等腰三角形.
如图,已知:CE=DF,AC=BD,∠1=∠2.求证:△GAB是等腰三角形.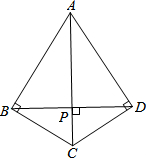 如图,四边形ABCD中,∠ABC=∠ADC=90°,BD⊥AC,垂足为P.
如图,四边形ABCD中,∠ABC=∠ADC=90°,BD⊥AC,垂足为P.