题目内容
15.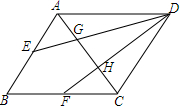 如图,在△ABC中,E,F分别为AB,BC边上的中点,G,H是AC的三等分点,EG,FH的延长线交于点D.求证:①DG:EG=2:1;②四边形ABCD是平行四边形.
如图,在△ABC中,E,F分别为AB,BC边上的中点,G,H是AC的三等分点,EG,FH的延长线交于点D.求证:①DG:EG=2:1;②四边形ABCD是平行四边形.
分析 ②连接BD交AC于O,连结BG,BH,首先证得四边形BHDG是平行四边形得到AO=OC,然后利用对角线互相平分的四边形是平行四边形判定即可.
①由平行四边形的性质得出AB=CD=2AE,AB∥CD,证出△CDG∽△AEG,得出对应边成比例,即可得出结论.
解答 证明:②连接BD交AC于O,连结BG,BH,如图所示: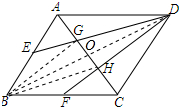
∵E是AB中点,AG=GH
∴AE=BE,EG是△ABH的一条中位线,
∴EG∥BH,即GD∥BH,
同理可证BG∥DH,
∴四边形BHDG是平行四边形.
∴BO=OD,GO=OH,
又∵AG=HC,
∴AG+GO=HC+OH,
即AO=OC,
又∵BO=OD,
∴四边形ABCD是平行四边形;
①∵四边形ABCD是平行四边形,
∴AB=CD=2AE,AB∥CD,
∴△CDG∽△AEG,
∴DG:EG=CD:AE=2:1.
点评 本题考查了平行四边形的判定与性质、三角形中位线定理、相似三角形的判定与性质;熟练掌握三角形中位线定理,证明四边形是平行四边形是解决问题的关键.

练习册系列答案
相关题目
4.小芳连续5天测得最低气温并整理后得出下表,
由于不小心被墨迹污染了两个数据,这两个数据分别是4,$\sqrt{2}$.
| 日期 | 一 | 二 | 三 | 四 | 五 | 标准差 | 平均气温 |
| 最低气温(℃) | 1 | 3 | 2 | 5 |  |  | 3 |
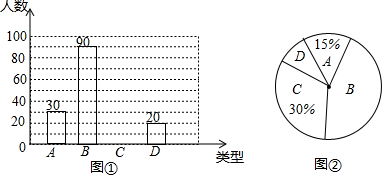
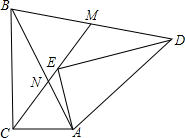 如图,Rt△ABC中,∠BCA=90°,∠BAC=α,将△ABC旋转一个角度后得到△AED,CE交AB于点N,交BD于点M.
如图,Rt△ABC中,∠BCA=90°,∠BAC=α,将△ABC旋转一个角度后得到△AED,CE交AB于点N,交BD于点M.