题目内容
3.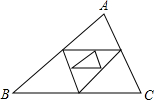 如下图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,依此类推,第2017个三角形周长为( )
如下图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边中点构成第三个三角形,依此类推,第2017个三角形周长为( )| A. | $\frac{1}{2016}$ | B. | $\frac{1}{2017}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
分析 根据三角形中位线定理、相似三角形的判定定理和性质定理计算即可.
解答 解:∵连结△ABC三边的中点构成第二个三角形,
由三角形中位线定理可知,第二个三角形与△ABC相似,且相似比为$\frac{1}{2}$,
同理第三个三角形与△ABC相似,且相似比为$\frac{1}{4}$=$\frac{1}{{2}^{2}}$,
则第2017个三角形周长为$\frac{1}{{2}^{2016}}$,
故选:C.
点评 本题考查的是三角形的中位线定理,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
13. 如图,菱形ABCD的对角线AC=3cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形ENCM的面积之比为( )
如图,菱形ABCD的对角线AC=3cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形ENCM的面积之比为( )
 如图,菱形ABCD的对角线AC=3cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形ENCM的面积之比为( )
如图,菱形ABCD的对角线AC=3cm,把它沿对角线AC方向平移1cm得到菱形EFGH,则图中阴影部分图形的面积与四边形ENCM的面积之比为( )| A. | 9:4 | B. | 12:5 | C. | 3:1 | D. | 5:2 |
11.下列各式计算正确的是( )
| A. | 6a+2a=8a2 | B. | (a-b)2=a2-b2 | C. | a4•a6=a10 | D. | (a3)2=a5 |
18. 如图,已知AB是⊙O的直径,∠CAB=50°,则∠D的度数为( )
如图,已知AB是⊙O的直径,∠CAB=50°,则∠D的度数为( )
 如图,已知AB是⊙O的直径,∠CAB=50°,则∠D的度数为( )
如图,已知AB是⊙O的直径,∠CAB=50°,则∠D的度数为( )| A. | 20° | B. | 40° | C. | 50° | D. | 70° |
8.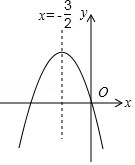 如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
①abc=0,②a+b+c>0,③a>b,④4ac-b2<0; 其中正确的结论有( )
 如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:
如图,已知二次函数 y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac-b2<0; 其中正确的结论有( )
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
15. 如图是一个几何体的三视图,则该几何体的展开图可以是( )
如图是一个几何体的三视图,则该几何体的展开图可以是( )
 如图是一个几何体的三视图,则该几何体的展开图可以是( )
如图是一个几何体的三视图,则该几何体的展开图可以是( )| A. |  | B. |  | C. |  | D. |  |