题目内容
4. 如图,梯形ABCD中,AD∥BC,BC=2AD,作DE∥AC交BA延长线于点E,CE、AD交于点F,求$\frac{DF}{BC}$的值.
如图,梯形ABCD中,AD∥BC,BC=2AD,作DE∥AC交BA延长线于点E,CE、AD交于点F,求$\frac{DF}{BC}$的值.
分析 延长BA和CD交于O,根据相似三角形的判定得出△OAD∽△OBC,△OED∽△OAC,△DEF∽△ACF,得出比例式,求出DF=$\frac{1}{6}$,即可得出答案.
解答 解:
延长BA和CD交于O,
∵AD∥BC,DE∥AC,
∴△OAD∽△OBC,△OED∽△OAC,
∴$\frac{AD}{BC}$=$\frac{OD}{OC}$,$\frac{DE}{AC}$=$\frac{OD}{OC}$,
∵BC=2AD,
∴$\frac{DE}{AC}$=$\frac{OD}{OC}$=$\frac{AD}{BC}$=$\frac{1}{2}$,
∵DE∥AC,
∴△DEF∽△ACF,
∴$\frac{DF}{AF}$=$\frac{DE}{AC}$=$\frac{1}{2}$,
∴DF=$\frac{1}{2}$AF=$\frac{1}{3}$AD=$\frac{1}{6}$BC,
即$\frac{DF}{BC}$=$\frac{1}{6}$.
点评 本题考查了相似三角形的性质和判定的应用,能根据相似得出比例是式是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.一项工程,甲单独做3天完成,乙单独做7天完成,两人共同合作,需x天完成,可列方程( )
| A. | 3x+7x=1 | B. | $\frac{x}{3}$+$\frac{x}{7}$=1 | C. | ($\frac{1}{3}$-$\frac{1}{7}$)x=1 | D. | x=($\frac{1}{3}$-$\frac{1}{7}$)-1 |
9.“相等的角是对顶角”是( )
| A. | 定义 | B. | 公理 | C. | 假命题 | D. | 定理 |
9.一个正比例函数的图象经过点(-2,4),它的表达式为( )
| A. | y=-2x | B. | y=2x | C. | y=-$\frac{1}{2}$x | D. | y=$\frac{1}{2}$x |
 已知数a、b、c在数轴上的位置如图所示,化简|a|+|b|+|a+b|-|b-c|.
已知数a、b、c在数轴上的位置如图所示,化简|a|+|b|+|a+b|-|b-c|.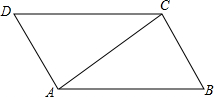 如图,AC是平行四边形ABCD的对角线.
如图,AC是平行四边形ABCD的对角线.