Question

18．如图，以BC为直径的圆交△ABC的两边AB、AC于点D、E，点E恰为AC的中点，BF为△ABC的外角平分线，点F在圆上，请你仅用一把无刻度的直尺，过点A作一条线段，将△ABC分成面积相等的两部分．

Answer 1

分析 利用等腰三角形的三线合一，判断出BE是∠ABC的平分线，进而判断出∠EBF=90°，再判断出四边形EBFC是矩形，点O为矩形对角线的交点即可．

解答 解：如图，连接BE，EF交直径BC于点O，即点O为圆的圆心，连接AO，即为所求作的线段．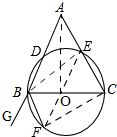

理由：∵BC为圆的直径，
∴BE⊥AC，
∵点E是AC中点，
∴∠ABE=∠CBE=$\frac{1}{2}$∠ABC，
∵BF为△ABC的外角的平分线，
∴∠CBF=$\frac{1}{2}$∠CBG，
∴∠EBF=∠EBC+∠CBF=$\frac{1}{2}$（∠ABC+∠CBG）=90°，
∵BC为直径，
∴∠BFC=90°，
∴∠BEC=∠EBF=∠BFC=90°，
∴四边形EBFC是矩形，
∴点O是BC中点，即：为圆心；
∴AO是△ABC的边BC中线，
即：AO将△ABC分成面积相等的两部分，

点评 此题是作图---复杂作图，主要考查了等腰三角形的性质，角平分线的性质，矩形的判定，判断出∠EBF=90°是解本题的关键．