题目内容
15.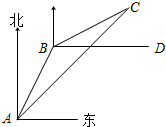 一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.5海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?
一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.5海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?
分析 过点B作BM⊥AH于M,过点C作CN⊥AH于N,利用直角三角形的性质求得CK的长,若CK>4.8则没有进入养殖场的危险,否则有危险.
解答  解:过点B作BM⊥AH于M,
解:过点B作BM⊥AH于M,
∴BM∥AF.
∴∠ABM=∠BAF=30°,
在△BAM中,AM=$\frac{1}{2}$AB=5,BM=5$\sqrt{3}$,
过点C作CN⊥AH于N,交BD于K,
在Rt△BCK中,∠CBK=90°-60°=30°,
设CK=x,则BK=$\sqrt{3}$x,
在Rt△ACN中,
∵在A处观测到东北方向有一小岛C,
∴∠CAN=45°,
∴AN=NC.
∴AM+MN=CK+KN,
又∵NM=BK,BM=KN,
∴x+5$\sqrt{3}$=5+$\sqrt{3}$x,
解得x=5,
∵5海里>4.8海里,
∴渔船没有进入养殖场的危险.
答:这艘渔船没有进入养殖场危险.
点评 本题主要考查了解直角三角形的应用-方向角问题,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
5.点(-2015,2015)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
3.下列事件是必然事件的是( )
| A. | 抛一枚硬币,正面朝上 | |
| B. | 抛一颗骰子,点数不大于6 | |
| C. | 到电影院任意买一张电影票,座位号是奇数 | |
| D. | 打开电视机,任选一个频道,屏幕上正在播放天气预报 |