题目内容
4.若$\sqrt{9{a}^{2}-6a+1}$=3a-1,则a的取值范围是a$≥\frac{1}{3}$.分析 根据$\sqrt{{a}^{2}}=a(a≥0)$可知:3a-1≥0,从而可解得a的取值.
解答 解:∵$\sqrt{9{a}^{2}-6a+1}=\sqrt{(3a-1)^{2}}$=3a-1,
∴3a-1≥0.
∴a$≥\frac{1}{3}$.
故答案为:a$≥\frac{1}{3}$.
点评 本题主要考查的是二次根式的性质,掌握公式$\sqrt{{a}^{2}}=a(a≥0)$是解题的关键,解答本题需要同学们注意公式成立的条件.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
14. 如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
(1)计算上述试验中“4朝下”的频率是0.27;
(2)投掷一次正四面体,出现2朝下的概率是$\frac{1}{4}$;
(3)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
 如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:| 朝下数字 | 1 | 2 | 3 | 4 |
| 出现的次数 | 20 | 10 | 14 | 16 |
(2)投掷一次正四面体,出现2朝下的概率是$\frac{1}{4}$;
(3)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
12.矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6cm,则BD的长( )
| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
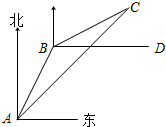 一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.5海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?
一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.5海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险? 如图,已知,AB∥CD,∠1=∠2,AE与EF平行吗?为什么?
如图,已知,AB∥CD,∠1=∠2,AE与EF平行吗?为什么? 如图,在长为10m,宽为8m的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽.
如图,在长为10m,宽为8m的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽. 如图,四边形ABCD内接于半径为4的⊙O,BD=4$\sqrt{3}$.
如图,四边形ABCD内接于半径为4的⊙O,BD=4$\sqrt{3}$.