题目内容
在△DEF中，DE=DF，EG为DF边上的高，∠DEG=70°，则∠EDF= ．
考点：等腰三角形的性质
专题：分类讨论
分析：根据题意分锐角三角形和钝角三角形作出图形，分类讨论即可求得答案．
解答：
解：如图1，当∠DEG=70°时，∠EDF=90°-∠DEG=90°-70°=20°；
如图2，当∠DEG=70°时，∠GDE=90°-∠DEG=20°，
则∠EDF=180°-∠GDE=180°-20°=60°，
故答案为：20°或160°．
解：如图1，当∠DEG=70°时，∠EDF=90°-∠DEG=90°-70°=20°；如图2，当∠DEG=70°时，∠GDE=90°-∠DEG=20°，
则∠EDF=180°-∠GDE=180°-20°=60°，
故答案为：20°或160°．
点评：本题考查了等腰三角形的性质，解题的关键是能够分类讨论，难度不大．
练习册系列答案
名校课堂系列答案
相关题目
方程
+
+…+
=1995的解是（ ）
| x |
| 1×2 |
| x |
| 2×3 |
| x |
| 1995×1996 |
| A、1995 | B、1996 |
| C、1997 | D、1998 |
如图，在等腰直角三角形ABC中，∠BAC=90°，在BC上截取BD=BA，作∠ABC的平分线与AD相交于点P，连结PC，若BD=2CD，△ABC的面积为2cm2，则△DPC的面积为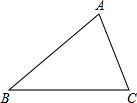
如图，已知△ABC．