题目内容
 如图,在等腰直角三角形ABC中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连结PC,若BD=2CD,△ABC的面积为2cm2,则△DPC的面积为
如图,在等腰直角三角形ABC中,∠BAC=90°,在BC上截取BD=BA,作∠ABC的平分线与AD相交于点P,连结PC,若BD=2CD,△ABC的面积为2cm2,则△DPC的面积为考点:等腰直角三角形,等腰三角形的性质
专题:
分析:根据等腰三角形三线合一的性质可得AP=PD,然后根据等底等高的三角形面积相等求出△BPC的面积等于△ABC面积的一半,根据不同底等高的△DPC的面积等于△BPC的面积的
代入数据计算即可得解.
| 1 |
| 3 |
解答:解:∵BD=BA,BP是∠ABC的平分线,
∴AP=PD,
∴S△BPD=
S△ABD,S△CPD=
S△ACD,
∴S△BPC=S△BPD+S△CPD=
S△ABD+
S△ACD=
S△ABC,
∵△ABC的面积为2cm2,
∴S△BPC=
×2=1cm2,
∵BD=2CD,
∴3DC=BC,
=
S△BPC=
.
故答案为
.
∴AP=PD,
∴S△BPD=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BPC=S△BPD+S△CPD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC的面积为2cm2,
∴S△BPC=
| 1 |
| 2 |
∵BD=2CD,
∴3DC=BC,
=
| 1 |
| 3 |
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评:本题考查了等腰三角形三线合一的性质,三角形的面积,利用等底等高的三角形的面积相等求出△BPC的面积与△ABC的面积的关系是解题的关键.

练习册系列答案
相关题目
 如图,函数y=-3x和y=kx+b的图象交与点A(m,4),则关于x的不等式kx+b+3x<0的解集为
如图,函数y=-3x和y=kx+b的图象交与点A(m,4),则关于x的不等式kx+b+3x<0的解集为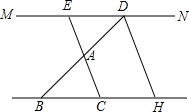 已知如图,MN∥BH,BD和EC交于点A,过点D作DH∥EC交BC延长线于点H.
已知如图,MN∥BH,BD和EC交于点A,过点D作DH∥EC交BC延长线于点H.
 小红第1至6周每周零花钱收支情况如图所示,6周后小红的零花钱一共还剩
小红第1至6周每周零花钱收支情况如图所示,6周后小红的零花钱一共还剩