题目内容
6. 如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=140°.
如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=140°.
分析 先根据平行线的性质,由l1∥l2得∠3=∠1=40°,再根据平行线的判定,由∠α=∠β得AB∥CD,然后根据平行线的性质得∠2+∠3=180°,再把∠1=40°代入计算即可.
解答 解:如图,
∵ l1∥l2,
l1∥l2,
∴∠3=∠1=40°,
∵∠α=∠β,
∴AB∥CD,
∴∠2+∠3=180°,
∴∠2=180°-∠3=180°-40°=140°.
故答案为140°.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.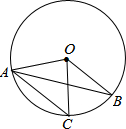 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )
如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )
 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )
如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )| A. | 25° | B. | 50° | C. | 60° | D. | 30° |
15.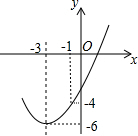 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),则下列结论中错误的是( )| A. | b2>4ac | |
| B. | ax2+bx+c≥-6 | |
| C. | 若点(-2,m),(-5,n)在抛物线上,则m>n | |
| D. | 关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1 |
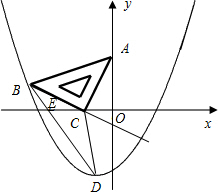 如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点A的坐标为(0,2),点B在抛物线y=ax2+ax-2上.
如图,在平面直角坐标系中,将一块等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(-1,0),点A的坐标为(0,2),点B在抛物线y=ax2+ax-2上. 如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=$\frac{3}{4}$x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴交于点C,直线l的解析式为y=$\frac{3}{4}$x+4,与x轴相交于点D,以点C为顶点的抛物线过点B.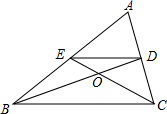 如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O,则$\frac{OB}{OD}$=2.
如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O,则$\frac{OB}{OD}$=2.