题目内容
19．一元二次方程x2+4x-3=0的两根为x1，x2，则x${\;}_{1}^{2}$+x${\;}_{2}^{2}$的值是（ ）| A． | 22 | B． | 24 | C． | 16 | D． | 10 |
分析 根据根与系数的关系可得出x1+x2=-4、x1•x2=-3，利用完全平方公式将${{x}_{1}}^{2}+{{x}_{2}}^{2}$转化为$（{x}_{1}+{x}_{2}）^{2}$-2x1•x2，代入数据即可得出结论．
解答 解：∵一元二次方程x2+4x-3=0的两根为x1，x2，
∴x1+x2=-4，x1•x2=-3，
∴${{x}_{1}}^{2}+{{x}_{2}}^{2}$=$（{x}_{1}+{x}_{2}）^{2}$-2x1•x2=（-4）2-2×（-3）=22．
故选A．
点评 本题考查了根与系数的关系，熟练掌握“x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$”是解题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
某中学为了解学生上学方式，现随机抽取部分学生进行调查，将结果绘成条形统计图如图，由此可估计该校2000名学生中有260名学生是乘车上学的．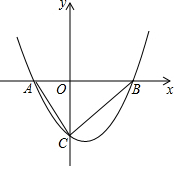
如图，已知二次函数y=x2-（$\sqrt{3}$-m）x-$\sqrt{3}$m（其中0＜m＜$\sqrt{3}$）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，△ABC的外心为P．
如图，在矩形ABCD中，E为BC上一点，连接DE，过点A作AF⊥DE于点F，△DEC与△ADF相似吗？请说明理由．
如图，在△ABC中，∠C=90°，AC=8，BD平分∠ABC交AC于D，AD：DC=3：1，则点D到AB的距离为（ ）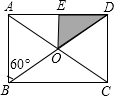
小明把如图所示的矩形纸板ABCD挂在墙上，E为AD中点，且∠ABD=60°，并用它玩飞镖游戏（每次飞镖均落在纸板上），击中阴影区域的概率是$\frac{1}{8}$．
8．正确的算式是（ ）
| A． | （-1）2011=-2011 | B． | 2（-3）2=36 | C． | -3÷$\frac{1}{2}$×2=-3 | D． | $\frac{1}{2}$÷（-$\frac{1}{2}$）=-1 |