题目内容
11．
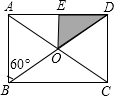小明把如图所示的矩形纸板ABCD挂在墙上，E为AD中点，且∠ABD=60°，并用它玩飞镖游戏（每次飞镖均落在纸板上），击中阴影区域的概率是$\frac{1}{8}$．
分析 先根据矩形的性质求出矩形对角线所分的四个三角形面积相等，再根据E为AD中点得出S△ODE=$\frac{1}{2}$S△OAD，进而求解即可．
解答 解：根据矩形的性质易证矩形的对角线把矩形分成的四个三角形均为同底等高的三角形，故其面积相等，
又∵E为AD中点，
∴S△ODE=$\frac{1}{2}$S△OAD，
∴S△ODE=$\frac{1}{8}$S矩形纸板ABCD，
∴击中阴影区域的概率是$\frac{1}{8}$．
故答案为$\frac{1}{8}$．
点评 此题主要考查了几何概率问题，用到的知识点为：概率=相应的面积与总面积之比．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
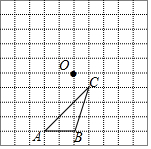如图所示，△ABC与点O在10×10的网格中的位置如图所示，设每个小正方形的边长为1．
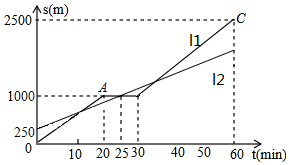小明和爸爸从家步行去公园，爸爸先出发一直匀速前行，小明后出发．家到公园的距离为2500m，如图是小明和爸爸所走路程s（m）与步行时间t（min）的函数图象．