��Ŀ����
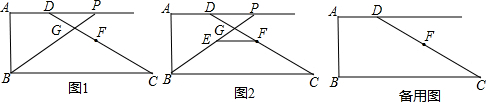
��֪����ͼ1��������ABCD�У���A=90�㣬AD��BC��AD=2��AB=3��tanC=
����P��AD�ӳ�����һ�㣬FΪDC���е㣬����BP�����߶�DF�ڵ�G��
��1������ABΪ�뾶�ġ�B����PDΪ�뾶�ġ�P���У���PD�ij���
��2����ͼ2������F��BC��ƽ���߽�BP�ڵ�E��
������DP=x��EF=y����y��x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ��
������DE��PF����DE=PF����PD�ij���
| 1 |
| 2 |
��1������ABΪ�뾶�ġ�B����PDΪ�뾶�ġ�P���У���PD�ij���
��2����ͼ2������F��BC��ƽ���߽�BP�ڵ�E��
������DP=x��EF=y����y��x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ��
������DE��PF����DE=PF����PD�ij���

���㣺�ı����ۺ���
ר�⣺
��������1����DP=x�����ɹ��ɶ�����ʾ��BP����ABΪ�뾶�ġ�B����PDΪ�뾶�ġ�P���У�����BP=AB+PD���г��������x��
��2��������DE���ӳ���BC�ڵ�M��FΪDC���е㣬EF��BC����DE=EM��CM=2EF�����ɡ�DEP�ա�MEB�õ�DP=BM����D��DH��BC�ڵ�H����tanC=
��CH=6��
��ΪAD=BH=2����BC=8����DP=x��EF=y��BC=BM+CM������x+2y=8�����ǵ�y=
(0��x��8)��
�ڵ�DP=EFʱ���ı���DEFPΪƽ���ı��Σ�����y=x��x=
���� DP��EFʱ���ı���DEFPΪ�������Σ���E��EQ��AP�ڵ�Q��DQ=
���ã�x=4������PD�ij�Ϊ
��4��
��2��������DE���ӳ���BC�ڵ�M��FΪDC���е㣬EF��BC����DE=EM��CM=2EF�����ɡ�DEP�ա�MEB�õ�DP=BM����D��DH��BC�ڵ�H����tanC=
| 1 |
| 2 |
��ΪAD=BH=2����BC=8����DP=x��EF=y��BC=BM+CM������x+2y=8�����ǵ�y=
| 8-x |
| 2 |
�ڵ�DP=EFʱ���ı���DEFPΪƽ���ı��Σ�����y=x��x=
| 8 |
| 3 |
| x-y |
| 2 |
| 8 |
| 3 |
����⣺��1������ֱ��������ABP�У�AD=2��AB=3��DP=x��
��BP=
��
����ABΪ�뾶�ġ�B����PDΪ�뾶�ġ�P���У�
��BP=AB+PD��
��
=3+x��
��ã�x=2��
��PD�ij�Ϊ2ʱ����ABΪ�뾶�ġ�B����PDΪ�뾶�ġ�P���У�
��2��������DE���ӳ���BC�ڵ�M��

��FΪDC���е㣬EF��BC��
��DE=EM��
��CM=2EF
��AD��BC���DEP�ա�MEB
��DP=BM��
��D��DH��BC�ڵ�H����tanC=
��DH=3��CH=6
��AD=BH=2��BC=8
��DP=x��EF=y��BC=BM+CM
��x+2y=8��
��y=
(0��x��8)��
�ڡ�AD��EF��DE=PF��
�� DP=EFʱ���ı���DEFPΪƽ���ı��Σ�
��y=x��
��x=
��
�� DP��EFʱ���ı���DEFPΪ�������Σ�

��E��EQ��AP�ڵ�Q��DQ=
��
��EQ��AB��BE=PE��
��AQ=
��
��DQ=
-2��
��
=
-2��
��ã�x=4��
��PD�ij�Ϊ
��4��
��BP=
| 32+(2+x)2 |
����ABΪ�뾶�ġ�B����PDΪ�뾶�ġ�P���У�
��BP=AB+PD��
��
| 32+(2+x)2 |
��ã�x=2��
��PD�ij�Ϊ2ʱ����ABΪ�뾶�ġ�B����PDΪ�뾶�ġ�P���У�
��2��������DE���ӳ���BC�ڵ�M��

��FΪDC���е㣬EF��BC��
��DE=EM��
��CM=2EF
��AD��BC���DEP�ա�MEB
��DP=BM��
��D��DH��BC�ڵ�H����tanC=
| 1 |
| 2 |
��AD=BH=2��BC=8
��DP=x��EF=y��BC=BM+CM
��x+2y=8��
��y=
| 8-x |
| 2 |
�ڡ�AD��EF��DE=PF��
�� DP=EFʱ���ı���DEFPΪƽ���ı��Σ�
��y=x��
��x=
| 8 |
| 3 |
�� DP��EFʱ���ı���DEFPΪ�������Σ�

��E��EQ��AP�ڵ�Q��DQ=
| x-y |
| 2 |
��EQ��AB��BE=PE��
��AQ=
| 2+x |
| 2 |
��DQ=
| 2+x |
| 2 |
��
| x-y |
| 2 |
| 2+x |
| 2 |
��ã�x=4��
��PD�ij�Ϊ
| 8 |
| 3 |
������������Ҫ������ƽ���ı��ε����ʣ����ε����ʣ�ȫ�������ε��ж��������Լ����ɶ�����Ӧ�ã�֪ʶ��Ƚ϶࣬�ۺ���ǿ��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
��֪a=
��b=
����a��b�Ĵ���ʽ��ʾ
���������ʽ�ǣ�������
| 2 |
| 5 |
| 20 |
| A��2a |
| B��ab2 |
| C��ab |
| D��a2b |
����y=
���Ա���x��ȡֵ��Χ�ǣ�������
| 3 | ||
|
| A��x��-3��x��0 |
| B��x��0 |
| C��x��-3 |
| D��x��-3��x��0 |
 ijͰװˮ��Ӫ��ÿ��ķ��⡢��Ա���ʵȹ̶��ɱ�Ϊ250Ԫ��ÿͰˮ�Ľ�����5Ԫ���涨���۵��۲��ø���12Ԫ/Ͱ��Ҳ���õ���7Ԫ/Ͱ�����鷢���վ�������p��Ͱ�������۵���x��Ԫ���ĺ���ͼ����ͼ��
ijͰװˮ��Ӫ��ÿ��ķ��⡢��Ա���ʵȹ̶��ɱ�Ϊ250Ԫ��ÿͰˮ�Ľ�����5Ԫ���涨���۵��۲��ø���12Ԫ/Ͱ��Ҳ���õ���7Ԫ/Ͱ�����鷢���վ�������p��Ͱ�������۵���x��Ԫ���ĺ���ͼ����ͼ�� ��֪����ƽ��ֱ������ϵxOy�У���A��x�Ḻ�����ϣ���B��y���������ϣ�OA=OB������y=-
��֪����ƽ��ֱ������ϵxOy�У���A��x�Ḻ�����ϣ���B��y���������ϣ�OA=OB������y=- ��ͼ��������ABCD������ֱ������ϵ�ڣ���֪A��3��3����AB=4��AD=3��������������ƽ��a����λ��������ƽ��a����λ��a��0�����þ���EFGH��
��ͼ��������ABCD������ֱ������ϵ�ڣ���֪A��3��3����AB=4��AD=3��������������ƽ��a����λ��������ƽ��a����λ��a��0�����þ���EFGH�� ��ͼ����֪����ABCD�ı߳�Ϊ2����B=60�㣬��P��Q�ֱ��DZ�BC��CD�ϵĶ��㣨����˵��غϣ�����BP=CQ��
��ͼ����֪����ABCD�ı߳�Ϊ2����B=60�㣬��P��Q�ֱ��DZ�BC��CD�ϵĶ��㣨����˵��غϣ�����BP=CQ��