题目内容
16.计算:已知|ab-2|+|a+1|=0,求式子的值.$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2016)(b+2016)}$.
分析 首先利用绝对值的性质得出a,b的值,进而利用分数的性质将原式变形求出答案.
解答 解:∵|ab-2|+|a+1|=0,
∴a=-1,b=-2,
∴原式=$\frac{1}{1×2}$+0+0+$\frac{1}{2}$+$\frac{1}{2×3}$+…+$\frac{1}{2014×2015}$
=1+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$
=1+$\frac{1}{2}$-$\frac{1}{2015}$
=$\frac{6043}{4030}$.
点评 此题主要考查了绝对值的性质以及分数的性质,正确将原式变形是解题关键.

练习册系列答案
相关题目
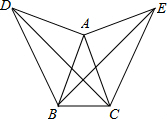 如图所示,在△ABC中,AB=AC,分别以AB,AC为直角边向外作两个等腰直角三角形△ABD和△ACE,使∠BAD=∠CAE=90°,求证:BE=CD.
如图所示,在△ABC中,AB=AC,分别以AB,AC为直角边向外作两个等腰直角三角形△ABD和△ACE,使∠BAD=∠CAE=90°,求证:BE=CD. 如图,AC∥BD,AF、BC相交于E,EF∥BD,求证:$\frac{1}{AC}$=$\frac{1}{BD}$-$\frac{1}{EF}$.
如图,AC∥BD,AF、BC相交于E,EF∥BD,求证:$\frac{1}{AC}$=$\frac{1}{BD}$-$\frac{1}{EF}$.