题目内容
3. 已知:如图,在△ABC中,∠B=60°,∠BAC=80°,AD⊥BC于D,AE平分∠DAC,求:∠DAE的度数.
已知:如图,在△ABC中,∠B=60°,∠BAC=80°,AD⊥BC于D,AE平分∠DAC,求:∠DAE的度数.
分析 先根据AD⊥BC可知∠BDA=90°,再由三角形内角和定理求出∠BAD的度数,由三角形外角的性质求出∠DAC的度数,根据角平分线的定义即可得出结论.
解答 解:∵AD⊥BC,
∴∠BDA=90°.
∵∠B=60°,
∴∠BAD=180°-90°-60°=30°.
∵∠BAC=80°,
∴∠DAC=∠BAC-∠BAD=80°-30°=50°.
∵AE平分∠DAC,
∴∠DAE=$\frac{1}{2}$∠DAC=25°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
14.某服装店销售每件进价为200元、170元的A、B两种品牌的上衣,下列是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种品牌上衣的销售单价;
(2)若超市准备用不多余5400元的金额再采购这两种品牌的上衣共30件,则A品牌的上衣最多能采购多少件?
| 销售时段 | 销售数量 | 销售收入 | |
| A品牌 | B品牌 | ||
| 第一周 | 3件 | 5件 | 1800元 |
| 第二周 | 4件 | 10件 | 3100元 |
(1)求A、B两种品牌上衣的销售单价;
(2)若超市准备用不多余5400元的金额再采购这两种品牌的上衣共30件,则A品牌的上衣最多能采购多少件?
11.下列长度的三条线段能组成三角形的是( )
| A. | 5,6,10 | B. | 5,6,11 | C. | 3,4,8 | D. | 4a,4a,8a(a>0) |
8.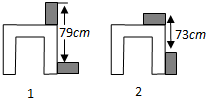 利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
 利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )| A. | 73cm | B. | 74cm | C. | 75cm | D. | 76cm |
15.七名学生的鞋号分别是:20,21,21,22,22,22,23.则这组数据的众数是( )
| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
13. 如图,直线a∥b,∠1=35°,那么∠2的度数是( )
如图,直线a∥b,∠1=35°,那么∠2的度数是( )
 如图,直线a∥b,∠1=35°,那么∠2的度数是( )
如图,直线a∥b,∠1=35°,那么∠2的度数是( )| A. | 40° | B. | 35° | C. | 55° | D. | 145° |