题目内容
20．已知⊙O直径为8，弦AB=4$\sqrt{2}$，则∠A0B=90°．分析 根据题意画出图形，过点O作OD⊥AB于点D，由垂径定理可得出AD的长，根据锐角三角函数的定义求出∠AOD的度数，进而可得出结论．
解答 
解：如图所示，
过点O作OD⊥AB于点D，
∵⊙O直径为8，弦AB=4$\sqrt{2}$，
∴OA=OB=4，AD=$\frac{1}{2}$AB=2$\sqrt{2}$，
∴sin∠AOD=$\frac{2\sqrt{2}}{4}$=$\frac{\sqrt{2}}{2}$，
∴∠AOD=45°，
∴∠AOB=2∠AOD=90°．
故答案为：90°．
点评 本题考查的是垂径定理，根据题意画出图形，利用数形结合求解是解答此题的关键．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
8．
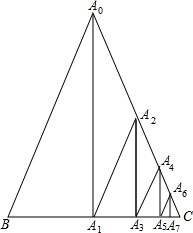如图所示，△A0BC为等腰三角形，在线段BC上，A1为BC中点，A3为A1C中点，A5为A3C中点，A7为A5C中点，…，在线段A0C上，A2为A0C中点，A4为A2C中点，A6为A4C中点…，依此下去，若BC=6，A0B=5，则线段AnAn+1（n＞0）的长度不可能为（ ）
如图所示，△A0BC为等腰三角形，在线段BC上，A1为BC中点，A3为A1C中点，A5为A3C中点，A7为A5C中点，…，在线段A0C上，A2为A0C中点，A4为A2C中点，A6为A4C中点…，依此下去，若BC=6，A0B=5，则线段AnAn+1（n＞0）的长度不可能为（ ）| A． | $\frac{5}{8}$ | B． | $\frac{1}{8}$ | C． | $\frac{1}{96}$ | D． | $\frac{5}{128}$ |