题目内容
8.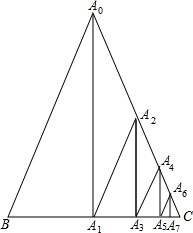 如图所示,△A0BC为等腰三角形,在线段BC上,A1为BC中点,A3为A1C中点,A5为A3C中点,A7为A5C中点,…,在线段A0C上,A2为A0C中点,A4为A2C中点,A6为A4C中点…,依此下去,若BC=6,A0B=5,则线段AnAn+1(n>0)的长度不可能为( )
如图所示,△A0BC为等腰三角形,在线段BC上,A1为BC中点,A3为A1C中点,A5为A3C中点,A7为A5C中点,…,在线段A0C上,A2为A0C中点,A4为A2C中点,A6为A4C中点…,依此下去,若BC=6,A0B=5,则线段AnAn+1(n>0)的长度不可能为( )| A. | $\frac{5}{8}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{96}$ | D. | $\frac{5}{128}$ |
分析 根据勾股定理求出A0A1的长度,根据三角形中位线定理表示出A1A2、A2A3的长度,根据规律总结得到答案.
解答 解:∵△A0BC为等腰三角形,A1为BC中点,
∴A1C=$\frac{1}{2}$BC=3,A0A1⊥BC,
由勾股定理得,A0A1=4,
∵A2为A0C中点,A3为A1C中点,
∴A2A3=$\frac{1}{2}$×4=2,
同理,A4A5=$\frac{1}{2}$×2=1,
∵A1为BC中点,A2为A0C中点,
∴A1A2=$\frac{1}{2}$×5,
依此下去,则线段AnAn+1为4×($\frac{1}{2}$)n或5×($\frac{1}{2}$)n,
则线段AnAn+1(n>0)的长度不可能为$\frac{1}{96}$,
故选:C.
点评 本题考查的是等腰三角形的性质、勾股定理和三角形的中位线定理,掌握三角形的中位线平行于第三边且等于第三边的一半是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 如图,在△ABC中,∠ACB=90°,CD是高,AC=4,BC=3,AB=5,求CD的长.
如图,在△ABC中,∠ACB=90°,CD是高,AC=4,BC=3,AB=5,求CD的长. 请画出△PAB的三条高.
请画出△PAB的三条高.