题目内容
 已知:如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
已知:如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.(1)以AB边上一点O为圆心,AD为弦作⊙O(要求用尺规作图,不写作法,保留作图痕迹);
(2)判断直线BC与⊙O的位置关系,并说明理由;
(3)若(1)中的⊙O的半径为2,⊙O与AB边的另一个交点为E,BD=2
| 3 |
考点:圆的综合题,平行线的判定与性质,切线的判定,扇形面积的计算,特殊角的三角函数值
专题:综合题
分析:(1)作线段AD的垂直平分线,交AB于点O,以点O为圆心,OA为半径作⊙O,如图1,⊙O即为所求作.
(2)连接OD,如图2.由OA=OD,AD平分∠CAB可证到∠ODA=∠CAD,从而有OD∥AC,进而可以证到OD⊥BC,即可得到直线BC与⊙O相切.
(3)连接OD,如图3.在Rt△ODB中运用三角函数可求出∠DOB的度数,就可求出扇形ODE的面积,就可求出所求图形面积.
(2)连接OD,如图2.由OA=OD,AD平分∠CAB可证到∠ODA=∠CAD,从而有OD∥AC,进而可以证到OD⊥BC,即可得到直线BC与⊙O相切.
(3)连接OD,如图3.在Rt△ODB中运用三角函数可求出∠DOB的度数,就可求出扇形ODE的面积,就可求出所求图形面积.
解答:解:(1)作线段AD的垂直平分线,交AB于点O,以点O为圆心,OA为半径作⊙O,如图1,

⊙O即为所求作.
(2)直线BC与⊙O相切.
证明:连接OD,如图2.

∵OA=OD,
∴∠OAD=∠ODA.
∵AD平分∠CAB,
∴∠BAD=∠CAD.
∴∠ODA=∠CAD.
∴OD∥AC.
∴∠ODB=∠ACB.
∵∠ACB=90°,
∴∠ODB=90°,即OD⊥BC.
∴直线BC与⊙O相切.
(3)连接OD,如图3,

则OD⊥BC(已证),阴影部分的面积就是所求图形的面积.
在Rt△ODB中,
∵OD=2,BD=2
,
∴tan∠DOB=
=
=
.
∴∠DOB=60°.
∴S扇形ODE=
=
.
∵S△ODB=
OD•DB=
×2×2
=2
,
∴S阴影=S△ODB=-S扇形ODE=2
-
.
∴线段BD、BE与劣弧DE所围成的图形面积为2
-
.

⊙O即为所求作.
(2)直线BC与⊙O相切.
证明:连接OD,如图2.

∵OA=OD,
∴∠OAD=∠ODA.
∵AD平分∠CAB,
∴∠BAD=∠CAD.
∴∠ODA=∠CAD.
∴OD∥AC.
∴∠ODB=∠ACB.
∵∠ACB=90°,
∴∠ODB=90°,即OD⊥BC.
∴直线BC与⊙O相切.
(3)连接OD,如图3,

则OD⊥BC(已证),阴影部分的面积就是所求图形的面积.
在Rt△ODB中,
∵OD=2,BD=2
| 3 |
∴tan∠DOB=
| BD |
| OD |
2
| ||
| 2 |
| 3 |
∴∠DOB=60°.
∴S扇形ODE=
| 60×π×22 |
| 360 |
| 2π |
| 3 |
∵S△ODB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S阴影=S△ODB=-S扇形ODE=2
| 3 |
| 2π |
| 3 |
∴线段BD、BE与劣弧DE所围成的图形面积为2
| 3 |
| 2π |
| 3 |
点评:本题考查了线段垂直平分线的作法、切线的判定、平行线的判定与性质、扇形的面积公式、特殊角的三角函数值、等腰三角形的性质、角平分线的定义等知识,有操作、有计算、有证明,具有一定的综合性,是一道好题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
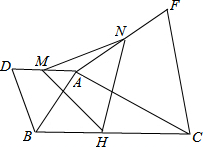 在△ABC中,以△ABC两侧作等边△ABD和等边△ACF,取AD和AF的中点M,N,再取BC的中点H,连接MN,MH,NH.推断并证明△MNH是什么三角形?
在△ABC中,以△ABC两侧作等边△ABD和等边△ACF,取AD和AF的中点M,N,再取BC的中点H,连接MN,MH,NH.推断并证明△MNH是什么三角形? 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y= △ABC中,∠ABC=45°,BD⊥AC,AD=2,CD=3,求BD长.
△ABC中,∠ABC=45°,BD⊥AC,AD=2,CD=3,求BD长. 如图,已知AE=CF,∠AFD=∠CEB,需要添加一个条件使△ADF≌△CBE,这个条件可以为
如图,已知AE=CF,∠AFD=∠CEB,需要添加一个条件使△ADF≌△CBE,这个条件可以为