题目内容
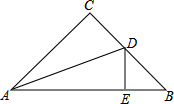 如图,在等腰直角△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于E,若AC=6,则△BDE的周长等于
如图,在等腰直角△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于E,若AC=6,则△BDE的周长等于考点:角平分线的性质,等腰直角三角形
专题:
分析:根据角平分线上的点到角的两边距离相等可得CD=DE,再利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应边相等可得AC=AE,然后求出△BDE的周长=AB,再根据等腰直角三角形的性质求出AB,即可得解.
解答:解:∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴CD=DE,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴△BDE的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB,
∵∠C=90°,AC=BC,
∴AB=
AC=6
,
∴△BDE的周长=6
.
故答案为:6
.
∴CD=DE,
在Rt△ACD和Rt△AED中,
|
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∴△BDE的周长=BD+DE+BE=BD+CD+BE=BC+BE=AC+BE=AE+BE=AB,
∵∠C=90°,AC=BC,
∴AB=
| 2 |
| 2 |
∴△BDE的周长=6
| 2 |
故答案为:6
| 2 |
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,等腰直角三角形的性质,熟记各性质并求出△BDE的周长=AB是解题的关键.

练习册系列答案
相关题目
数轴上表示整数的点称为整点,某数轴的单位长度为1cm,若在这个数轴上随意划出一条长2010cm的线段AB,则线段AB盖住的整点有( )
| A、2009个 |
| B、2010个 |
| C、2010个或2009个 |
| D、2010个或2011个 |
 不等式组解集如图所示,则其解集为( )
不等式组解集如图所示,则其解集为( )| A、0≤x<1 | B、x<1 |
| C、x≤0 | D、0<x<1 |
 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,直至得C14,若P(41,m)在这列抛物线上,则m=
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,直至得C14,若P(41,m)在这列抛物线上,则m=