题目内容
11．一个不透明的袋子中有10个黑球，若干个白球，它们除颜色外，完全相同，小明从袋中随机一次摸出10个，记下其中黑球的数目后，再把它们放回，搅匀后重复上述过程20次，发现共摸到25个黑球，由此可以估计袋中的白球数约为70个．分析 由于共摸球20次，发现共有黑球25个，即200个球里面有25个黑球，若袋中的白球有x个，则$\frac{10}{10+x}$=$\frac{25}{10×20}$，然后解方程即可．
解答 解：设袋中的白球有x个，根据题意得$\frac{10}{10+x}$=$\frac{25}{10×20}$，
解得x=70．
故估计出袋中的白球是70个，
故答案为：70．
点评 本题考查了用样本估计总体和利用频率估计概率：大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．
练习册系列答案
相关题目
某校学生参加体育兴趣小组情况的统计图如图所示，已知参加人数最少的小组有50人，则参加人数最多的小组人数为90．
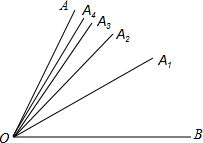如图，已知∠AOB=m度，OA1平分∠AOB，OA2平分∠AOA1，OA3平分∠AOA2，OA4平分∠AOA3，…，OAn平分∠AOAn-1，则∠AOAn的度数为$\frac{1}{{2}^{n}}m$度．
如图所示，如果点A的位置为（3，2），那么点B的位置为（2，5），点C的位置为（4，4）
A、B两站（视为直线）相距25km，C、D为两村庄（视为两个点），DA⊥AB于A，CB⊥于B．已知DA=15km，CB=10km，现在要在建设一个土特产品收购站E，使得C、D两村到E站的距离相等，则E站应建在距A站多远处？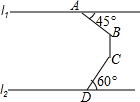
如图，在同一平面内，两条平行景观长廊l1和l2间有一条“U”形通道，其中AB段与景观长廊l1成45°角，长为20m；BC段与景观长廊垂直，长为10m，CD段与景观长廊l2成60°角，长为10m，求两景观长廊间的距离（结果保留根号）
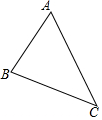已知△ABC如图所示，求作一个△A′B′C′，使△A′B′C′≌△ABC，并写出△A′B′C′与△ABC全等的理由：SAS．（请用尺规作图）