题目内容
6．当式子|x-1|+|x-2|+|x-3|+…+|x-1999|取得最小值时，实数x的值是（ ）| A． | 1 | B． | 999 | C． | 1000 | D． | 1999 |
分析 观察已知条件可以发现，|x-a|表示x到a的距离．要使题中式子取得最小值，则应该找出与最小数和最大数距离相等的x的值，此时式子得出的值则为最小值．
解答 解：由已知条件可知，|x-a|表示x到a的距离，只有当x到1的距离等于x到1999的距离时，式子取得最小值．
所以当x=$\frac{1+1999}{2}$=1000时，式子取得最小值．
故选C．
点评 本题考查了绝对值，做此题需要一定的技巧，要结合绝对值的定义来考虑．另外还要知道，当x与最小数和最大数距离相等时，式子才能取得最小值．
练习册系列答案
智慧小复习系列答案
相关题目
14．
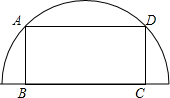如图，一个长为2、宽为1的矩形ABCD内接于半圆O，矩形的长BC在半圆半径上，则半圆O的面积为（ ）
如图，一个长为2、宽为1的矩形ABCD内接于半圆O，矩形的长BC在半圆半径上，则半圆O的面积为（ ）| A． | $\frac{π}{2}$ | B． | $\frac{2π}{3}$ | C． | π | D． | 2π |
18．下列不等式，是一元一次不等式的是（ ）
| A． | x+y＜x+2 | B． | x2-2x-1 | C． | $\frac{1}{2}$$+\frac{1}{3}$＞$\frac{1}{6}$ | D． | 2（1-y）+y＞4y+2 |
15．一元二次方程6x2-7x+1=0的两个根是（ ）
| A． | x1=-$\frac{1}{6}$，x2=1 | B． | x1=$\frac{1}{6}$，x2=-1 | C． | x1=$\frac{1}{6}$，x2=1 | D． | x1=-$\frac{1}{6}$，x2=-1 |
16．计算a7•a3的结果是（ ）
| A． | a4 | B． | a10 | C． | a21 | D． | a73 |