题目内容
9.已知$a={(-2)^0}\;,b={(\frac{1}{2})^{-1}}\;,c={(-2)^{-2}}$,那么a、b、c的大小关系为c<a<b.分析 首先求出a、b、c的大小,然后根据正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,据此判断即可.
解答 解:a=(-2)0=1,b=${(\frac{1}{2})}^{-1}$=2,${c=(-2)}^{-2}=-\frac{1}{4}$,
∵-$\frac{1}{4}<1<2$,
∴c<a<b.
故答案为:c<a<b.
点评 (1)此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
(2)此题还考查了零指数幂:a0=1(a≠0),以及负整数指数幂的计算,要熟练掌握.

练习册系列答案
相关题目
18.如果am=3,an=6,则a2m+n等于( )
| A. | 15 | B. | 36 | C. | 12 | D. | 54 |
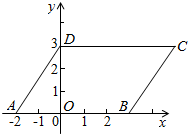 如图,四边形ABCD为平行四边形,OD=3,CD=AB=5,点A坐标为(-2,0)
如图,四边形ABCD为平行四边形,OD=3,CD=AB=5,点A坐标为(-2,0)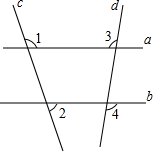 如图所示,∠1+∠2=180°,∠3=100°,则∠4等于100°.
如图所示,∠1+∠2=180°,∠3=100°,则∠4等于100°.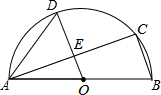 如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.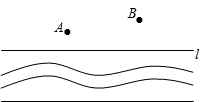 如图,政府决定实施“引河入村”的工程,需将河水经A村引入B村,要使修渠路线最短,水泵站的位置P应建在河边的什么地方,并画出水渠的修建路线.
如图,政府决定实施“引河入村”的工程,需将河水经A村引入B村,要使修渠路线最短,水泵站的位置P应建在河边的什么地方,并画出水渠的修建路线.