题目内容
18．
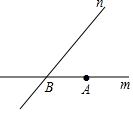如图，直线m，n交于点B，m、n的夹角为50°，点A是直线m上的点，在直线n上寻找一点C，使△ABC是等腰三角形，这样的C点有多少个？（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 分别以∠A、∠B、∠C为顶角进行讨论即可求得答案．
解答 解：
∵△ABC为等腰三角形，
∴分三种情况：
①当以∠C为顶角时，则有BC=AC，即点C在线段AB的垂直平分线上，可知满足条件；
②当以∠A为顶角时，则有AC=AB，由两直线夹角为50°，可知此时点C只能在直线m的上方，有一个点；
③当以∠B为顶角时，则有AB=CB，此时点C可以在直线m的上方，也可以在直线n的上方，有两个点，
综上可知满足条件的C点有4个，
故选D．
点评 本题主要考查等腰三角形的判定，由条件确定出点C的位置是解题的关键，注意分类讨论．
练习册系列答案
相关题目
8．等腰三角形的两边长为1和3，则周长为（ ）
| A． | 7 | B． | 5 | C． | 7或5 | D． | 无法确定 |
9．下列对于-34，叙述正确的是（ ）
| A． | 读作-3的4次幂 | B． | 底数是-3，指数是4 | ||
| C． | 表示4个3相乘的积的相反数 | D． | 表示4个-3相乘的积 |
6．下列说法中：
①-a一定是负数；
②倒数等于它本身的数是±1；
③几个有理数相乘，当负因数有奇数个时，积为负；
④几个有理数相乘，当积为负时，负因数有奇数个．
其中正确的个数有（ ）
①-a一定是负数；
②倒数等于它本身的数是±1；
③几个有理数相乘，当负因数有奇数个时，积为负；
④几个有理数相乘，当积为负时，负因数有奇数个．
其中正确的个数有（ ）
| A． | 1个 | B． | 2个? | C． | 3个 | D． | 4个 |
13．方程2x2-4x+1=0化成（x+m）2=n（n≥0）的形式是（ ）
| A． | （x-1）2=$\frac{1}{2}$ | B． | （2x-1）2=$\frac{1}{2}$ | C． | （x-1）2=0 | D． | （x-2）2=3 |
3．
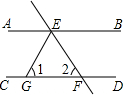如图，已知AB∥CD，直线EF分别交AB，CD于点E、F，EG平分∠AEF，若∠2=50°，则∠1的度数是（ ）
如图，已知AB∥CD，直线EF分别交AB，CD于点E、F，EG平分∠AEF，若∠2=50°，则∠1的度数是（ ）| A． | 70° | B． | 65° | C． | 60° | D． | 50° |
在正△ABC内有一点P，PA=2，PB=2$\sqrt{3}$，PC=4，则CB的长为2$\sqrt{7}$．
7．如果向东走10米记作+10米，那么-5米表示（ ）
| A． | 向南走5米 | B． | 向西走-5米 | C． | 向西走5米 | D． | 向东走5米 |
8．
如图，点A、B、C都在⊙O上，若∠AOB+∠ACB=90°，则∠ACB的大小是（ ）
如图，点A、B、C都在⊙O上，若∠AOB+∠ACB=90°，则∠ACB的大小是（ ）| A． | 20° | B． | 25° | C． | 30° | D． | 40° |