题目内容
13. 如图,△ABC中,D是AB上一点,已知∠ACD=∠B,AD=4,AB=9,则AC长为( )
如图,△ABC中,D是AB上一点,已知∠ACD=∠B,AD=4,AB=9,则AC长为( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 只要证明△ADC∽△ACB,可得AC:AB=AD:AC,即AC2=AB•AD,将数值代入计算即可求出AC的长.
解答 解:在△ADC与△ACB中,
∵∠ABC=∠ACD,∠A=∠A,
∴△ACD∽△ABC;
∴AC:AB=AD:AC,
∴AC2=AB•AD,
∵AD=4,AB=9,
∴AC2=4×9=36,
∴AC=6,
故选B
点评 本题考查的是相似三角形的判定与性质,灵活运用所学知识解决问题是解题的关键,属于基础题,中考常考题型.

练习册系列答案
相关题目
3.下列结论中,正确的是( )
| A. | 过任意三点一定能画一条直线 | B. | 两点之间线段最短 | ||
| C. | 射线AB和射线BA是同一条射线 | D. | 经过一点的直线只有一条 |
4.若关于x的分式方程$\frac{x-m}{x}$=m-2无解,则m的值为( )
| A. | 0 | B. | 0或3 | C. | 3 | D. | ±2 |
8.已知a+b=4,c-d=3,则(b+c)-(d-a)的值等( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
5.反比例函数y=$\frac{-4}{x}$的图象位于( )
| A. | 第一、三象限 | B. | 第三、四象限 | C. | 第一、二象限 | D. | 第二、四象限 |
2.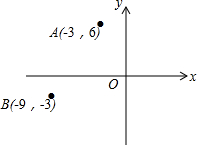 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
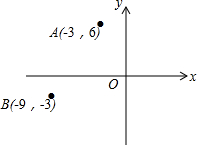 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )| A. | (-1,2) | B. | (-1,2)或(1,-2) | C. | (-9,18) | D. | (-9,18)或(9,-18) |
3.联合国在2016年10月17日发出警告,2030年之前因气候变迁而增加的贫困人口可能高达12.2亿人,其中又以南亚和非洲受害人数最多,用科学记数法表示12.2亿正确的是( )
| A. | 1.22×109 | B. | 1.22×1010 | C. | 12.2×109 | D. | 122×108 |
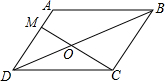 如图,在?ABCD中,AM=$\frac{1}{3}$AD,BD与MC相交于点O,则S△MOD:S△COD=2:3.
如图,在?ABCD中,AM=$\frac{1}{3}$AD,BD与MC相交于点O,则S△MOD:S△COD=2:3.