题目内容
 如图,以△ABC的边AB为直径作⊙O,分别交AC、BC于点D、E,过点D作DF⊥BC于F点,且D为
如图,以△ABC的边AB为直径作⊙O,分别交AC、BC于点D、E,过点D作DF⊥BC于F点,且D为 |
| AE |
| BE |
| AB |
| 3 |
| 5 |
| 5 |
考点:垂径定理,勾股定理,圆周角定理
专题:
分析:连接AE交OD于H,根据圆周角的性质求得AE⊥BE,根据垂径定理求得OD⊥AE,从而求得OD∥BC,进而求得OH=
BE,根据题意设BE=3x,则AB=5x,由勾股定理得,AE=4x,进而得出AH=2x,OH=1.5x,DH=x,然后根据勾股定理求得AD=
x,又因为AD=4
,即可求得x=4,进而求得⊙O的半径.
| 1 |
| 2 |
| 5 |
| 5 |
解答: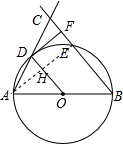 解:连接AE交OD于H,
解:连接AE交OD于H,
∵AB是⊙O的直径,
∴∠AEB=90°,
即AE⊥BE,
∵D为
的中点,
∴OD⊥AE,
∴OD∥BC,
∵OA=OB,
∴OH=
BE,
在RT△ABE中,
=
,设BE=3x,则AB=5x,由勾股定理得,AE=4x,
∴AH=2x,OH=1.5x,
∴DH=OD-OH=2.5x-1.5x=x,
在RT△ADH中,AD=
=
=
x,
∵AD=4
,
∴x=4,
∴⊙O的半径=4×2.5=10.
 解:连接AE交OD于H,
解:连接AE交OD于H,∵AB是⊙O的直径,
∴∠AEB=90°,
即AE⊥BE,
∵D为
 |
| AE |
∴OD⊥AE,
∴OD∥BC,
∵OA=OB,
∴OH=
| 1 |
| 2 |
在RT△ABE中,
| BE |
| AB |
| 3 |
| 5 |
∴AH=2x,OH=1.5x,
∴DH=OD-OH=2.5x-1.5x=x,
在RT△ADH中,AD=
| AH2+DH2 |
| (2x)2+x2 |
| 5 |
∵AD=4
| 5 |
∴x=4,
∴⊙O的半径=4×2.5=10.
点评:本题考查了圆周角定理、垂径定理、勾股定理的应用,熟练掌握这些定理是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图,△ABC中,D在BC上,∠DAC=∠B,CE为∠ACB的角平分线,CE交AD于F,已知BD=3,DC=1,求
如图,△ABC中,D在BC上,∠DAC=∠B,CE为∠ACB的角平分线,CE交AD于F,已知BD=3,DC=1,求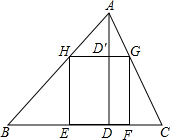 在一底为8米,高为6米的三角形钢板上剪一个面积最大的矩形.
在一底为8米,高为6米的三角形钢板上剪一个面积最大的矩形.