题目内容
18.在直角坐标系中,一直线a向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转60°后所得直线经过点B(-$\sqrt{3}$,0),则直线a的函数关系式为y=-$\sqrt{3}$x+6.分析 先用待定系数法求出直线AB的解析式为y=$\sqrt{3}$x+3,再由题意,知直线b经过A(0,3),($\sqrt{3}$,0),求出直线b的解析式为y=-$\sqrt{3}$x+3,然后将直线b向上平移3个单位后得直线a,根据上加下减的平移规律即可求出直线a的解析式.
解答 解:如图
设直线AB的解析式为y=kx+b,
∵A(0,3),B(-$\sqrt{3}$,0),
∴$\left\{\begin{array}{l}{b=3}\\{-\sqrt{3}k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=3}\end{array}\right.$,
∴直线AB的解析式为y=$\sqrt{3}$x+3.
由题意,知直线y=$\sqrt{3}$x+3绕点A逆时针旋转60°后得到直线b,则直线b经过A(0,3),($\sqrt{3}$,0),
易求直线b的解析式为y=-$\sqrt{3}$x+3,
将直线b向上平移3个单位后得直线a,所以直线a的解析式为y=-$\sqrt{3}$x+3+3,即y=-$\sqrt{3}$x+6.
故答案为y=-$\sqrt{3}$x+6.
点评 本题考查了一次函数图象与几何变换,解决本题的关键是得到把直线y=$\sqrt{3}$x+3绕点A逆时针旋转60°后得到直线b的解析式.

练习册系列答案
相关题目
8.如果把分式$\frac{2x}{x+y}$中的x和y都扩大2倍,那么分式的值( )
| A. | 不变 | B. | 扩大2倍 | C. | 扩大4倍 | D. | 缩小2倍 |
6.不等式3(x-2)<7的正整数解有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
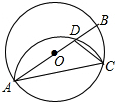 如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为40度.
如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为40度.