题目内容
3.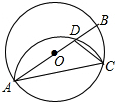 如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为40度.
如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为40度.
分析 首先连接BC,由AB是直径,可求得∠ACB=90°,则可求得∠B的度数,然后由翻折的性质可得,$\widehat{AC}$所对的圆周角为∠B,$\widehat{ABC}$所对的圆周角为∠ADC,继而求得答案.
解答  解:连接BC,
解:连接BC,
∵AB是直径,
∴∠ACB=90°,
∵∠BAC=25°,
∴∠B=90°-∠BAC=90°-25°=65°,
根据翻折的性质,$\widehat{AC}$所对的圆周角为∠B,$\widehat{ABC}$所对的圆周角为∠ADC,
∴∠ADC+∠B=180°,
∴∠B=∠CDB=65°,
∴∠DCA=∠CDB-∠A=65°-25°=40°.
故答案为:40.
点评 此题考查了圆周角定理以及折叠的性质.注意掌握辅助线的作法,能得到∠BDC=∠B是解此题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
8.为防治雾霾,保护环境,合肥上下掀起“爱绿护绿”热潮,建好后的大蜀山森林公园将真正成为“合肥绿肺”,经过两年时间,绿地面积增加了21%,这两年绿地面积的平均增长率是( )
| A. | 12% | B. | 30% | C. | 10% | D. | 22% |
13.下列图形,既是中心对称图形,又是轴对称图形的是( )
| A. | 等边三角形 | B. | 平行四边形 | C. | 正五边形 | D. | 正六边形 |
 如图,点A、B、C在⊙O上,且∠AOB=120°,则∠A+∠B=60°.
如图,点A、B、C在⊙O上,且∠AOB=120°,则∠A+∠B=60°.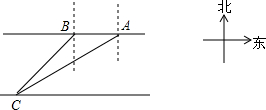 一次数学活动课上,老师带领学生去测一条东西流向的河宽,如图所示,小明在河北岸点A处观测到河对岸有一点C在A的南偏西59°的方向上,沿河岸向西前行20m到达B处,又测得C在B的南偏西45°的方向上,请你根据以上数据,帮助小明计算出这条河的宽度.(参考数据:tan31°≈$\frac{3}{5}$,sin31°≈$\frac{1}{2}$)
一次数学活动课上,老师带领学生去测一条东西流向的河宽,如图所示,小明在河北岸点A处观测到河对岸有一点C在A的南偏西59°的方向上,沿河岸向西前行20m到达B处,又测得C在B的南偏西45°的方向上,请你根据以上数据,帮助小明计算出这条河的宽度.(参考数据:tan31°≈$\frac{3}{5}$,sin31°≈$\frac{1}{2}$)