题目内容
将下列式子化为部分分式:
(1)
(2)
(3)
(4)
.
(1)
| 2x2+x+2 |
| x2+1 |
(2)
| x2+1 |
| (x+1)2(x+2) |
(3)
| 12x2+20x-29 |
| (2x-1)(4x2-4x-15) |
(4)
| 2x2+x+2 |
| x3+3 |
考点:分式的加减法
专题:计算题
分析:(1)根据整式的加减,把分子分成含分母的部分,可得答案;
(2)根据分式的加减,先通分,可得答案;
(3)根据异分母分式的加减,先通分,可得答案;
(4)根据分式的加减,把分母分成两项,可得答案.
(2)根据分式的加减,先通分,可得答案;
(3)根据异分母分式的加减,先通分,可得答案;
(4)根据分式的加减,把分母分成两项,可得答案.
解答:解:(1)
=
=2+
;
(2)
=
+
;
(3)原式=
-
+
;
(4)原式=
+
.
| 2x2+x+2 |
| x2+1 |
| 2(x2+1)+x |
| x2+1 |
| x |
| x2+1 |
(2)
| x2+1 |
| (x+1)2(x+2) |
| -x-2 |
| (x+1)2 |
| 2 |
| x+2 |
(3)原式=
| 1 |
| 2x-1 |
| 1 |
| 2x+3 |
| 3 |
| 2x-5 |
(4)原式=
| 2x2 |
| x3+3 |
| x+2 |
| x2+3 |
点评:本题考查了分式的加减,利用了分式的加减.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
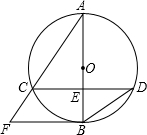 如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC=
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC= 如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为
如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为