题目内容
 如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为
如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为考点:圆周角定理,坐标与图形性质,勾股定理
专题:
分析:利用圆周角定理可以判定BC是⊙A的直径,则由勾股定理来求该圆的直径即可.
解答: 解:如图,连接BC.
解:如图,连接BC.
∵∠COB=90°,且点O、C、B三点都在圆A上,
∴BC是△OBC的直径.
又B(8,0),C(0,6),
∴BC=
=10,
∴⊙A的半径为 5.
故答案是:5.
 解:如图,连接BC.
解:如图,连接BC.∵∠COB=90°,且点O、C、B三点都在圆A上,
∴BC是△OBC的直径.
又B(8,0),C(0,6),
∴BC=
| 82+62 |
∴⊙A的半径为 5.
故答案是:5.
点评:本题考查了圆周角定理、坐标与图形性质以及勾股定理.证得BC是圆A的直径是解题的关键.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
a是有理数,下列说法正确的是( )
| A、a表示正数 |
| B、-a表示负数 |
| C、|a|表示正数 |
| D、a2是非负数 |
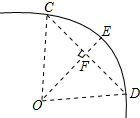 如图,一条公路的转弯处是一段圆弦(即图中
如图,一条公路的转弯处是一段圆弦(即图中
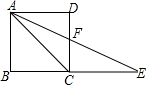 如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:①∠E=22.5°; ②∠AFC=112.5°; ③∠ACE=135°;④AC=CE;⑤AD:CE=1:2.其中正确的有
如图,正方形ABCD中,点E在BC的延长线上,AE平分∠DAC,则下列结论:①∠E=22.5°; ②∠AFC=112.5°; ③∠ACE=135°;④AC=CE;⑤AD:CE=1:2.其中正确的有