题目内容
14．关于x，y的二元二次方程组$\left\{\begin{array}{l}{x^2}+y=2\\ 2x+y=m\end{array}\right.$有且只有一组实数解，则m的值是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 将两式相减，消去y，得到关于x的一元二次方程，由方程组有且只有一组实数解，可得关于x的一元二次方程有两个相等的实数根，从而得到根的判别式为0，就可求出m的值．
解答 解：将两式相减，可得
x2-2x=2-m，
整理得x2-2x+m-2=0，
由题可得（-2）2-4（m-2）=0，
解得m=3．
故选C．
点评 本题考查的是根的判别式的应用，将方程组有唯一解转化为关于x的一元二次方程有两个相等的实数根，是解决本题的关键．
练习册系列答案
相关题目
如图，圆O的半径为6，点A、B、C在圆O上，且∠ACB=45°，则点O到弦AB的距离为3$\sqrt{2}$．
5．已知二次函数y=2（x+a）2+b的顶点坐标为（2，-3），则a，b的值分别为（ ）
| A． | 2，-3 | B． | -2，-3 | C． | 2，3 | D． | -2，3 |
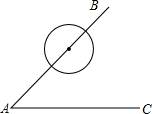如图所示，∠BAC=60°，O是射线AB上一点，以O为圆心，$\frac{1}{2}$OA的长为半径的⊙O，将AC绕点A逆时针旋转30°时，AC与⊙O相切．
如图，写出图中的所有角，并比较它们的大小，然后指出哪些角是直角，哪些角是锐角，哪些角是钝角．
如图，在△ABC中，D是BC边中点，DE⊥DF交AB于点E，DF交AC于点F．若CF2+BE2=EF2，求证：AB2+AC2=BC2．
如图，四边形ABCD中，AD∥BC，AC，BD交于点O，过点O作EF分别交AB，CD于E，F，且EF∥BC，求证：OE=OF．
3．
如图，若∠AOB=∠COD，那么（ ）
如图，若∠AOB=∠COD，那么（ ）| A． | ∠1＞∠2 | B． | ∠1＜∠2 | ||
| C． | ∠1=∠2 | D． | ∠1、∠2的大小不确定 |