题目内容
4.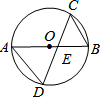 如图,AB是⊙O的直径,它与弦CD交于点E.我们给出下列结论:
如图,AB是⊙O的直径,它与弦CD交于点E.我们给出下列结论:①AE•BE=CE•DE;②△ADE∽△CBE;③∠A=∠C;④∠AED=∠BEC
这些结论中正确的是( )
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ②③④ |
分析 根据圆周角定理得到∠A=∠C,∠D=∠B,由相似三角形的判定定理得到△AED∽△CEB,再根据相似三角形的性质得到AE•BE=CE•DE,由对顶角的性质得到∠AED=∠BEC.
解答 解:∵AB是⊙O的直径,它与弦CD交于点E,
∴∠A=∠C,∠D=∠B,
∴△AED∽△CEB,
∴$\frac{AE}{CE}=\frac{DE}{BE}$,
∴AE•BE=CE•DE,
∵∠AED与∠BEC是对顶角,
∴∠AED=∠BEC,
∴①②③④都正确.
故选A.
点评 本题考查了相似三角形的判定和性质,圆周角定理,对顶角相等,熟练掌握圆周角定理是解题的关键.

练习册系列答案
相关题目
16.在代数式3a-2b,$\frac{x+1}{{x}^{2}+1}$,$\frac{1}{3}$(a-b),$\frac{2}{m}$,$\frac{{x}^{2}-{y}^{2}}{x+y}$,$\frac{1}{π}$中,分式有( )
| A. | 1个 | B. | 3个 | C. | 2个 | D. | 4个 |
14.高为4cm且底面为正方形的长方体的体积为196cm2,则该长方体的表面积为( )
| A. | 200cm2 | B. | 210cm2 | C. | 220cm2 | D. | 294cm2 |
 如图,在边长为1的正方形纸板上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的长方形彩色纸片(n为大于1的整数),请你用“数形结合”的思想,依数形变化的规律,计算
如图,在边长为1的正方形纸板上,依次贴上面积为$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$,…,$\frac{1}{{2}^{n}}$的长方形彩色纸片(n为大于1的整数),请你用“数形结合”的思想,依数形变化的规律,计算