题目内容
19.若∠A与∠B的两边分别垂直,请判断这两个角的等量关系.(1)如图1,∠A与∠B的关系是∠A=∠B;如图2,∠A与∠B的关系是∠A+∠B=180°;
(2)若∠A与∠B的两边分别平行,试探索这两个角的等量关系,画图并证明你的结论.
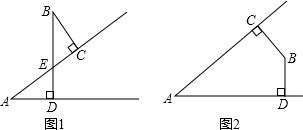
分析 (1)根据垂直的量相等的角都等于90°,对顶角相等,所以∠A=∠B,同样根据垂直的量相等的角都等于90°,根据四边形的内角和等于360°,所以∠A+∠B=360°-90°-90°=180°.所以如果一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是相等或互补;
(2)根据平行线的性质得到同位角相等,同旁内角互补即可得到结论.
解答 (1)如图1,∠A=∠B,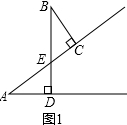
∵∠ADE=∠BCE=90°,∠AED=∠BEC,
∴∠A=180°-∠ADE-∠AED,
∠B=180°-∠BCE-∠BEC,
∴∠A=∠B,
如图2,∠A+∠B=180°;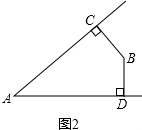
∴∠A+∠B=360°-90°-90°=180°.
∴∠A与∠B的等量关系是互补;
故答案为:∠A=∠B,∠A+∠B=180°;
(2)如图3,∠A=∠B,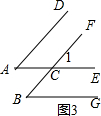
∵AD∥BF,∴∠A=∠1,
∵AE∥BG,∴∠1=∠B,
∴∠A=∠B;
如图4,∠A+∠B=180°,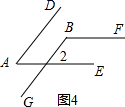
∵AD∥BG,
∴∠A=∠2,
∵AE∥BF,
∴∠2+∠B=180°,
∴∠A+∠B=180°.
点评 本题考查了平行线的性质,垂线的定义,四边形的内角和等于360°,三角形的内角和等于180°,对顶角相等,正确掌握各性质定理是解题的关键.

练习册系列答案
相关题目
10.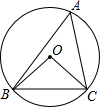 如图,⊙O是△ABC的外接圆,∠BCO=40°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BCO=40°,则∠A的度数等于( )
 如图,⊙O是△ABC的外接圆,∠BCO=40°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BCO=40°,则∠A的度数等于( )| A. | 60° | B. | 50° | C. | 45° | D. | 40° |
14.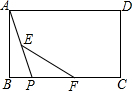 如图,矩形ABCD中,点P从点B出发沿BC向点C运动,E、F分别是AP、PC的中点,则EF的长度( )
如图,矩形ABCD中,点P从点B出发沿BC向点C运动,E、F分别是AP、PC的中点,则EF的长度( )
 如图,矩形ABCD中,点P从点B出发沿BC向点C运动,E、F分别是AP、PC的中点,则EF的长度( )
如图,矩形ABCD中,点P从点B出发沿BC向点C运动,E、F分别是AP、PC的中点,则EF的长度( )| A. | 逐渐增大 | B. | 逐渐减小 | C. | 不变 | D. | 无法确定 |
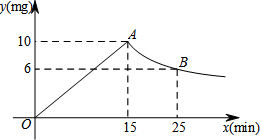 据媒体报道,近期“甲型H7N9禽流感”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“甲型H7N9禽流感”,对教室进行“熏药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示,第一段是线段OA,第二段是一个反比例函数的图象(即图中A点及其右侧的部分),根据图象所示信息,解答下列问题:
据媒体报道,近期“甲型H7N9禽流感”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“甲型H7N9禽流感”,对教室进行“熏药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示,第一段是线段OA,第二段是一个反比例函数的图象(即图中A点及其右侧的部分),根据图象所示信息,解答下列问题: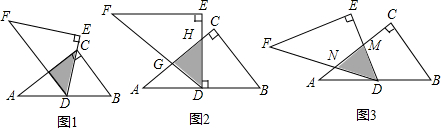
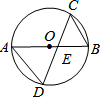 如图,AB是⊙O的直径,它与弦CD交于点E.我们给出下列结论:
如图,AB是⊙O的直径,它与弦CD交于点E.我们给出下列结论: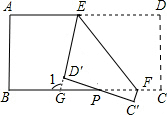 如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠BFC′=70°,则∠1=110°.
如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交于点G.若∠BFC′=70°,则∠1=110°.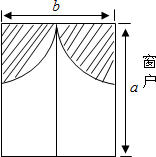 小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成:
小明房间窗户的装饰物如图所示,它们由两个四分之一圆组成: