题目内容
11.先化简再求值:已知a2+2a-1=0,求$({\frac{a-2}{{{a^2}+2a}}-\frac{a-1}{{{a^2}+4a+4}}})÷\frac{a-4}{a+2}$的值.分析 先根据分式混合运算的法则把原式进行化简,再根据a2+2a-1=0得出a2+2a=1,代入原式进行计算即可.
解答 解:原式=[$\frac{a-2}{a(a+2)}$-$\frac{a-1}{(a+2)^{2}}$]•$\frac{a+2}{a-4}$
=$\frac{{a}^{2}-4-{a}^{2}+a}{{a(a+2)}^{2}}$•$\frac{a+2}{a-4}$
=$\frac{a-4}{{a(a+2)}^{2}}$•$\frac{a+2}{a-4}$
=$\frac{1}{{a(a+2)}^{\;}}$
=$\frac{1}{{a}^{2}+2a}$,
∵a2+2a-1=0,
∴a2+2a=1,
∴原式=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
6.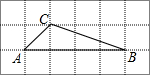 如图,A,B,C三点在正方形网络线的交点处,则tanB的值为( )
如图,A,B,C三点在正方形网络线的交点处,则tanB的值为( )
 如图,A,B,C三点在正方形网络线的交点处,则tanB的值为( )
如图,A,B,C三点在正方形网络线的交点处,则tanB的值为( )| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{{\sqrt{10}}}{3}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
3.估计$\sqrt{5}$-1的值在哪两个整数之间( )
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |

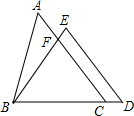 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,∠D=60°,∠ABE=28°,则∠ACB=46°.
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,∠D=60°,∠ABE=28°,则∠ACB=46°.