题目内容
16.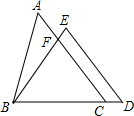 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,∠D=60°,∠ABE=28°,则∠ACB=46°.
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,∠D=60°,∠ABE=28°,则∠ACB=46°.
分析 根据全等三角形的判定与性质,可得∠ACB与∠DBE的关系,根据三角形外角的性质,可得答案.
解答 解:在△ABC和△DEB中,
$\left\{\begin{array}{l}{AC=BD}\\{AB=ED}\\{BC=BE}\end{array}\right.$,
∴△ABC≌△DEB (SSS),
∴∠ACB=∠DBE.
∵∠AFB是△BFC的外角,
∴∠ACB+∠DBE=∠AFB,
∠ACB=$\frac{1}{2}$∠AFB=46°.
故答案为:46°.
点评 本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,三角形外角的性质.

练习册系列答案
相关题目
1. 在平面直角坐标系xOy中,已知点A(2,3),在x轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有( )个.
在平面直角坐标系xOy中,已知点A(2,3),在x轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有( )个.
 在平面直角坐标系xOy中,已知点A(2,3),在x轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有( )个.
在平面直角坐标系xOy中,已知点A(2,3),在x轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有( )个.| A. | 4 | B. | 5个 | C. | 7个 | D. | 8个 |
8.若△ABC∽△DEF,△ABC与△DEF的相似比为1:3,则S△ABC:S△DEF为( )
| A. | 1:3 | B. | 1:9 | C. | 1:$\sqrt{3}$ | D. | 3:1 |
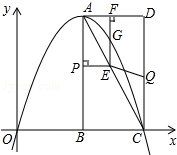 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.