题目内容
如图,在边长为1个单位长度的小正方形组成的网格中,已知AB∥CD,分别探讨下面三个图形中∠BAP与∠APC、∠DCP的关系,请任选一个加以说明.


考点:平行线的性质
专题:几何图形问题
分析:(1)过P作PE∥AB,则AB∥CD,利用两直线平行,同旁内角互补即可求解;
(2)过P作PF∥AB,则PF∥CD,利用两直线平行,内错角相等以及角的和差即可求解;
(3)过P作PF∥AB,则PF∥CD,利用两直线平行,内错角相等以及角的和差即可求解.
(2)过P作PF∥AB,则PF∥CD,利用两直线平行,内错角相等以及角的和差即可求解;
(3)过P作PF∥AB,则PF∥CD,利用两直线平行,内错角相等以及角的和差即可求解.
解答: 答:(1)∠BAP+∠DCP+∠APC=360°.
答:(1)∠BAP+∠DCP+∠APC=360°.
证明:过P作PE∥AB,则AB∥CD,
∵AB∥PE,
∴∠PAB+∠APE=180°,
∵PE∥CD,
∴∠DCP+∠CPE=180°,
∴∠PAB+∠APE+∠DCP+∠CPE=360°,
即∠BAP+∠DCP+∠APC=360°;
(2)∠BAP+∠DCP=∠APC,
证明:过P作PF∥AB,则PF∥CD.
∵PF∥AB,
∴∠APF=∠BAP,
同理∠CPF=∠DCF,
又∵∠APC=∠APF+∠CPF,
∴∠BAP+∠DCP=∠APC;
(3)∠BAP-∠DCP=∠APC,
证明:过P作PF∥AB,则PF∥CD.
∵PF∥AB,
∴∠APF=∠BAP,
同理∠CPF=∠DCF,
又∵∠APC=∠APF-∠CPF,
∴∠BAP-∠DCP=∠APC.
 答:(1)∠BAP+∠DCP+∠APC=360°.
答:(1)∠BAP+∠DCP+∠APC=360°.证明:过P作PE∥AB,则AB∥CD,
∵AB∥PE,
∴∠PAB+∠APE=180°,
∵PE∥CD,
∴∠DCP+∠CPE=180°,
∴∠PAB+∠APE+∠DCP+∠CPE=360°,
即∠BAP+∠DCP+∠APC=360°;
(2)∠BAP+∠DCP=∠APC,
证明:过P作PF∥AB,则PF∥CD.
∵PF∥AB,
∴∠APF=∠BAP,
同理∠CPF=∠DCF,
又∵∠APC=∠APF+∠CPF,
∴∠BAP+∠DCP=∠APC;
(3)∠BAP-∠DCP=∠APC,
证明:过P作PF∥AB,则PF∥CD.
∵PF∥AB,
∴∠APF=∠BAP,
同理∠CPF=∠DCF,
又∵∠APC=∠APF-∠CPF,
∴∠BAP-∠DCP=∠APC.
点评:本题利用了平行线的性质:两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目
若方程(m-1)x2+2mx+m=0有两个不相等的实数根,则m的取值范围为( )
| A、m>0 |
| B、m≥0 |
| C、m>0且m≠1 |
| D、以上答案都不对 |
 如图,在湖边一座楼房顶上观察湖面上空一只悬浮的气球,直接观察时,仰角 α=30°,观察湖中气球倒影时,俯角为β=45°,房顶离湖面高度为h=10m,求气球离湖面的高度H.
如图,在湖边一座楼房顶上观察湖面上空一只悬浮的气球,直接观察时,仰角 α=30°,观察湖中气球倒影时,俯角为β=45°,房顶离湖面高度为h=10m,求气球离湖面的高度H. 如图所示,已知⊙O1与⊙O2外切于点E.求证:若⊙O1的直径AB与⊙O2的直径CD平行,则直线AD和BC相交于点E.
如图所示,已知⊙O1与⊙O2外切于点E.求证:若⊙O1的直径AB与⊙O2的直径CD平行,则直线AD和BC相交于点E.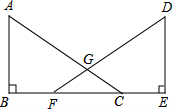 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:∠BFG=∠ECG.
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:∠BFG=∠ECG.