题目内容
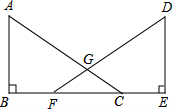 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:∠BFG=∠ECG.
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE.求证:∠BFG=∠ECG.考点:全等三角形的判定与性质
专题:证明题
分析:由BF=CE,利用等式的性质得到BC=EF,利用HL得到直角三角形ABC与直角三角形DEF全等,利用全等三角形对应角相等得到一对角相等,再利用等角的补角相等即可得证.
解答:证明:∵BF=CE,
∴BF+FC=CE+FC,即BC=EF,
在Rt△ABC和Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ACB=∠DFE,
∴∠BFG=∠ECG.
∴BF+FC=CE+FC,即BC=EF,
在Rt△ABC和Rt△DEF中,
|
∴Rt△ABC≌Rt△DEF(HL),
∴∠ACB=∠DFE,
∴∠BFG=∠ECG.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
已知y=1-
,z=1-
,则用含x的代数式表示y为( )
| 1 |
| z |
| 1 |
| x |
A、y=
| ||
B、x=
| ||
C、y=
| ||
D、x=
|
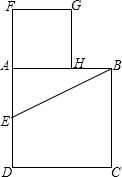 已知线段AB,按照如下的方法作图:以AB为边作正方形ABCD,取AD的中点E,连接EB,延长DA到F,使EF=EB,以线段AF为边,作正方形AFGH,那么点H是线段AB的黄金分割点吗?请说明理由.
已知线段AB,按照如下的方法作图:以AB为边作正方形ABCD,取AD的中点E,连接EB,延长DA到F,使EF=EB,以线段AF为边,作正方形AFGH,那么点H是线段AB的黄金分割点吗?请说明理由.
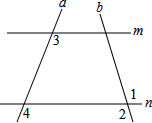 如图,直线a,b,被直线m,n所截,且∠1=∠2,求证:∠3=∠4(填空).
如图,直线a,b,被直线m,n所截,且∠1=∠2,求证:∠3=∠4(填空).
 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.