题目内容
 已知:如图,四边形ABCD是梯形,AD∥BC,E、F分别是AB、CD边上的中点,求证:EF∥AD,EF=
已知:如图,四边形ABCD是梯形,AD∥BC,E、F分别是AB、CD边上的中点,求证:EF∥AD,EF=| AD+BC |
| 2 |
考点:梯形中位线定理,三角形中位线定理
专题:证明题
分析:连接AF并延长,交BC延长线于点M,证明△ADF≌△MCF,判断EF是△ABM的中位线,继而可得出结论.
解答: 证明:连接AF并延长,交BC延长线于点M,
证明:连接AF并延长,交BC延长线于点M,
在△ADF和△MCF中,
,
∴△ADF≌△MCF(ASA),
∴AF=FM,AD=CM,
∴EF是△ABM的中位线,
∴EF∥BC∥AD,EF=
BM=
(BC+AD).
 证明:连接AF并延长,交BC延长线于点M,
证明:连接AF并延长,交BC延长线于点M,在△ADF和△MCF中,
|
∴△ADF≌△MCF(ASA),
∴AF=FM,AD=CM,
∴EF是△ABM的中位线,
∴EF∥BC∥AD,EF=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形及梯形的中位线定理,作出辅助线是解题关键,三角形及梯形的中位线定理需要我们熟练记忆.

练习册系列答案
相关题目
要使二次根式
在实数范围内有意义,则x的取值范围是( )
| x-1 |
| A、x<1 | B、x≤1 |
| C、x>1 | D、x≥1 |
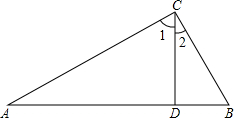 如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( )
如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是( )| A、∠2与∠A互余 |
| B、∠l=∠B |
| C、∠l和∠B都是∠A的余角 |
| D、∠2=∠A |

 如图,圆上一点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,求阴影部分的面积.
如图,圆上一点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,求阴影部分的面积.