题目内容
 如图,圆上一点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,求阴影部分的面积.
如图,圆上一点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,求阴影部分的面积.考点:勾股定理,圆周角定理
专题:
分析:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径,依此根据勾股定理可得AB的长,再根据阴影部分的面积=正方形的面积-半圆的面积即可求解.
解答:解:∵∠AEB=90°,AE=6,BE=8,
∴AB=
=10,
∴阴影部分的面积为:
10×10-π×(10÷2)2÷2
=100-π×25÷2
=100-12.5π.
∴AB=
| 62+82 |
∴阴影部分的面积为:
10×10-π×(10÷2)2÷2
=100-π×25÷2
=100-12.5π.
点评:考查了圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径,勾股定理,正方形的面积计算,以及半圆的面积计算.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
下列计算正确的是( )
| A、(a+2)(a-2)=a2-2 |
| B、(1+3a)(1-3b)=1-9ab |
| C、(x+1)(x-2)=x2-x-2 |
| D、(x-y)2=x2-y2 |
 已知:如图,四边形ABCD是梯形,AD∥BC,E、F分别是AB、CD边上的中点,求证:EF∥AD,EF=
已知:如图,四边形ABCD是梯形,AD∥BC,E、F分别是AB、CD边上的中点,求证:EF∥AD,EF= 已知△ABC以及边AB的中心对称线段A′B′,先确定对称中心O再画全△ABC的中心对称图形△A′B′C′.
已知△ABC以及边AB的中心对称线段A′B′,先确定对称中心O再画全△ABC的中心对称图形△A′B′C′.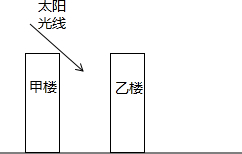 甲楼楼高50米,乙楼坐落在甲楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为30°,此时,求:
甲楼楼高50米,乙楼坐落在甲楼的正北面,已知当地冬至中午12时太阳光线与水平面的夹角为30°,此时,求: 如图,已知线段a、b、c,用圆规和直尺作线段,使它等于a+2b-c.
如图,已知线段a、b、c,用圆规和直尺作线段,使它等于a+2b-c.