题目内容
 如图,在一个正方形网格中有一个△ABC(定点都在格点上).
如图,在一个正方形网格中有一个△ABC(定点都在格点上).①在网格中画出△ABC向右平移5个单位,再向下平移3各单位得到的△A1B1C1.
②连接AA1、BB1,求正方形AA1B1B的面积.
③估计正方形AA1B1B的边长在哪两个整数之间?
考点:作图-平移变换,勾股定理
专题:
分析:①根据图形平移的性质画出△A1B1C1即可;
②连接AA1、BB1,根据勾股定理求出AB的长,由正方形的面积公式即可得出结论;
③估算出AB的长即可.
②连接AA1、BB1,根据勾股定理求出AB的长,由正方形的面积公式即可得出结论;
③估算出AB的长即可.
解答: 解:①如图所示:
解:①如图所示:
②∵由勾股定理可知,AB=
=
,
∴S正方形AA1B1B=(
)2=34;
③由②知AB=
,
∵25<34<36,
∴5<
<6,即5<AB<6.
 解:①如图所示:
解:①如图所示:②∵由勾股定理可知,AB=
| 32+52 |
| 34 |
∴S正方形AA1B1B=(
| 34 |
③由②知AB=
| 34 |
∵25<34<36,
∴5<
| 34 |
点评:本题考查的是作图-平移变换,熟知图形平移的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,小丽从O点出发,先向西走20米,再向北走30米到达点M,如果点M的位置用(-20,30)表示,那么(20,-30)表示的位置是( )
如图,小丽从O点出发,先向西走20米,再向北走30米到达点M,如果点M的位置用(-20,30)表示,那么(20,-30)表示的位置是( ) 如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于F.
如图,已知∠ABC=180°-∠A,BD⊥CD于D,EF⊥CD于F.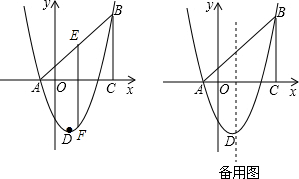
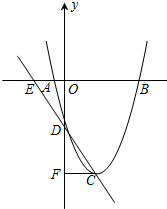 已知抛物线y=
已知抛物线y=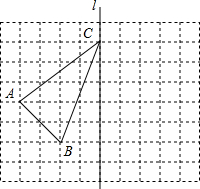 如图,在方格纸中,每个小正方形的边长为1,有一个格点△ABC(即三角形的顶点都在格点上),点C在直线l上.
如图,在方格纸中,每个小正方形的边长为1,有一个格点△ABC(即三角形的顶点都在格点上),点C在直线l上. 在△ABC中,∠A=60°,∠ABC、∠ACB所对的b、c满足:b2+c2-2(b+c)+2=0.
在△ABC中,∠A=60°,∠ABC、∠ACB所对的b、c满足:b2+c2-2(b+c)+2=0.