题目内容
18．已知|7-3m|+（n-5）2=3m-7-2$\sqrt{m-3}$，求m-n的值．分析 先变形为|7-3m|+（n-5）2+2$\sqrt{m-3}$=3m-7，根据非负数的性质可得3m-7≥0，计算绝对值可得（n-5）2+2$\sqrt{m-3}$=0，再根据非负数的性质得到m，n的值，再代入计算即可求解．
解答 解：|7-3m|+（n-5）2=3m-7-2$\sqrt{m-3}$，
|7-3m|+（n-5）2+2$\sqrt{m-3}$=3m-7，
则3m-7≥0，
3m-7+（n-5）2+2$\sqrt{m-3}$=3m-7，
（n-5）2+2$\sqrt{m-3}$=0，
则n-5=0，m-3=0，
解得n=5，m=3，
则m-n=3-5=-2．
点评 本题考查了非负数的性质，关键是熟悉几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
20．
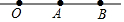如图，O，A，B三点在同一直线上，则下列说法中正确的是（ ）
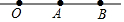如图，O，A，B三点在同一直线上，则下列说法中正确的是（ ）| A． | 射线OA与射线AO表示同一条射线 | B． | 射线OA大于射线AB | ||
| C． | 射线OA与射线OB表示同一条射线 | D． | 线段OA与线段AO表示两条不同线段 |
6．
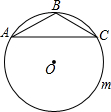如图，△ABC中，AB=BC，∠ABC=120°，AC=2$\sqrt{3}$，⊙O是△ABC的外接圆，D是优弧AmC上任意一点（不包括A，C），记四边形ABCD的周长为y，BD的长为x，则y关于x的函数关系式是（ ）
如图，△ABC中，AB=BC，∠ABC=120°，AC=2$\sqrt{3}$，⊙O是△ABC的外接圆，D是优弧AmC上任意一点（不包括A，C），记四边形ABCD的周长为y，BD的长为x，则y关于x的函数关系式是（ ）| A． | y=$\frac{\sqrt{3}}{4}$x+4 | B． | y=$\sqrt{3}$x+4 | C． | y=$\sqrt{3}$x2+4 | D． | y=$\frac{\sqrt{3}}{4}$x2+4 |
8．下列分式中，最简分式是（ ）
| A． | $\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-xy}$ | B． | $\frac{x+1}{{x}^{2}-1}$ | ||
| C． | $\frac{{x}^{2}-1}{{x}^{2}+1}$ | D． | $\frac{{x}^{2}-36}{2x+12}$ |