题目内容
用三种不同的正多边形地砖铺满地面,若其中有正三角形,正八边形,则另一个为正 边形.
考点:平面镶嵌(密铺)
专题:
分析:分别求出各个正多边形的每个内角的度数,结合镶嵌的条件即可求出答案.
解答:解:∵正三角形的内角是60°,正八边形的内角是135°,
∴另一个正多边形的内角是165°,
∴另一个正多边形是24边形;
故答案为:24.
∴另一个正多边形的内角是165°,
∴另一个正多边形是24边形;
故答案为:24.
点评:本题考查了平面镶嵌,几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
若x+m与2-x的乘积中不含x的一次项,则实数m的值为( )
| A、-2 | B、2 | C、0 | D、1 |
下列图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
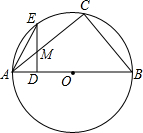 如图,AB是⊙O的直径,点C、E在
如图,AB是⊙O的直径,点C、E在