题目内容
1．下列说法：①-$\sqrt{17}$是17的平方根；
②$\frac{1}{27}$的立方根是±$\frac{1}{3}$；
③-81没有立方根；
④互为相反数的两个数的立方根也互为相反数，
错误的有（ ）
| A． | ①③ | B． | ①④ | C． | ②③ | D． | ②④ |
分析 依据平方根、立方根的定义进行解答即可．
解答 解：①-$\sqrt{17}$是17的平方根，故①正确；
②$\frac{1}{27}$的立方根是$\frac{1}{3}$，故②错误；
③负数有立方根，故③错误；
④互为相反数的两个数的立方根也互为相反数，故④正确．
故选：C．
点评 本题主要考查的是立方根、平方根的性质，熟练掌握相关性质是解题的关键．
练习册系列答案
导学教程高中新课标系列答案
相关题目
11．下列图形中是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
12．把64开平方得（ ）
| A． | 8 | B． | -8 | C． | ±8 | D． | 32 |
9．已知抛物线的解析式为y=-2（x-2）2+1，则当 x≥2时，y随x增大的变化规律是（ ）
| A． | 增大 | B． | 减小 | C． | 先增大再减小 | D． | 先减小后增大 |
如图，已知AB∥CD，O是∠BAC与∠ACD的平分线的交点．OE⊥AC于E，OE=2，则点O到AB与CD的距离之和为4．
13．小张同学说出了二次函数的两个条件：
（1）当x＜1时，y随x的增大而增大；
（2）函数图象经过点（-2，4）．
则符合条件的二次函数表达式可以是（ ）
（1）当x＜1时，y随x的增大而增大；
（2）函数图象经过点（-2，4）．
则符合条件的二次函数表达式可以是（ ）
| A． | y=-（x-1）2-5 | B． | y=2（x-1）2-14 | C． | y=-（x+1）2+5 | D． | y=-（x-2）2+20 |
10．一次函数y=kx+b，当-3≤x≤1时，对应的y的值为1≤y≤9，则kb的值为（ ）
| A． | 14 | B． | -6 | C． | -4或21 | D． | -6或14 |
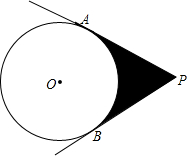如图，PA，PB是⊙O的两条切线，切点分别为A，B，⊙O的半径为2cm，∠P=60°，求图中阴影部分的面积．