题目内容
 在△ABC中,点O为边AB,AC的垂直平分线的交点,请写出∠BOC和∠A的数量关系.
在△ABC中,点O为边AB,AC的垂直平分线的交点,请写出∠BOC和∠A的数量关系.考点:线段垂直平分线的性质
专题:
分析:连接OA,根据线段垂直平分线上的点到两端点的距离相等可得OA=OB=OC,根据等边对等角可得∠OAB=∠OBA,∠OAC=∠OCA,再利用三角形的内角和等于180°表示出∠OBC+∠OCB,然后根据三角形的内角和定理列式整理即可得解.
解答: 解:连接OA,∵点O为边AB,AC的垂直平分线的交点,
解:连接OA,∵点O为边AB,AC的垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∴∠OBA+∠OCA=∠A,
在△ABC中,∠OBC+∠OCB=180°-(∠OAB+∠OBA+∠OAC+∠OCA)=180°-2∠A,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-(180°-2∠A)=2∠A,
即∠BOC=2∠A.
 解:连接OA,∵点O为边AB,AC的垂直平分线的交点,
解:连接OA,∵点O为边AB,AC的垂直平分线的交点,∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,
∴∠OBA+∠OCA=∠A,
在△ABC中,∠OBC+∠OCB=180°-(∠OAB+∠OBA+∠OAC+∠OCA)=180°-2∠A,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-(180°-2∠A)=2∠A,
即∠BOC=2∠A.
点评:本题考查了线段垂直平分线上的点到两端点的距离相等的性质,等边对等角的性质,三角形的内角和定理,熟记性质是解题的关键.

练习册系列答案
相关题目
 如图,直线y=2x-4分别交x轴、y轴于B、A两点,交双曲线y=
如图,直线y=2x-4分别交x轴、y轴于B、A两点,交双曲线y=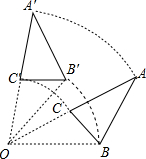 如图,将三角形ABC绕点O旋转得到三角形A′B′C′,且∠AOB=30°,∠AOB′=20°,则:
如图,将三角形ABC绕点O旋转得到三角形A′B′C′,且∠AOB=30°,∠AOB′=20°,则: 如图,河岸边CD的同侧有A,B两个村庄,现在河岸边CD修一个水电站P,是铺设连接A,B两村的管道最短,水站P应建在何处?
如图,河岸边CD的同侧有A,B两个村庄,现在河岸边CD修一个水电站P,是铺设连接A,B两村的管道最短,水站P应建在何处? 如图,在菱形ABCD中 菱形ABCD的边长为2
如图,在菱形ABCD中 菱形ABCD的边长为2