题目内容
如图,AO=BO=6厘米,OC是一条射线,OC⊥AB.一动点P从点A以1厘米/秒的速度向点B爬行,另一动点Q从点O以2厘米/秒的速度沿射线OC方向爬行,它们同时出发,当点P到达B点时点Q也停止运动.设运动时间为t秒.
(1)直接写出OQ= (用t的代数式).
(2)经过多少秒,△POQ的面积为8平方厘米.
(3)当t= 时,△PBQ为等腰三角形(直接写出答案)
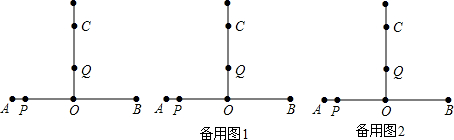
(1)直接写出OQ=
(2)经过多少秒,△POQ的面积为8平方厘米.
(3)当t=

考点:一元二次方程的应用
专题:几何动点问题
分析:(1)由路程=速度×时间就可以直接得出结论;
(2)由三角形的面积公式,分情况讨论,当P在AO上和P在BO上分别计算出结论;
(3)当PB=BQ时,由勾股定理表示出BQ,然后建立方程求出其解即可.
(2)由三角形的面积公式,分情况讨论,当P在AO上和P在BO上分别计算出结论;
(3)当PB=BQ时,由勾股定理表示出BQ,然后建立方程求出其解即可.
解答:解:(1)由函数图象,得
OQ=2t,
故答案为:2t;
(2)当P在AO上,
=8,
解得:t1=2,t2=4.
∵t1=2,t2=4在0<t<6范围内,
∴t1=2,t2=4.
P在BO上,
=8,
解得:t3=3+
,t4=3-
.
∵t3=3+
在6<t<12范围内,
∴t3=3+
;
(3)在Rt△BOQ中,由勾股定理,得
BQ2=4t2+36,
BP=12-t,BP2=144-24t+t2,
∵△PBQ是等腰三角形,
∴PB=BQ,
∴PB2=BQ2,
∴4t2+36=144-24t+t2,
解得:t1=-4+2
,t2=-4-2
(舍去).
当PB=PQ时,BP2=144-24t+t2,PQ2=4t2+(12-t)2,
无解.
故答案为:-4+2
.
OQ=2t,
故答案为:2t;
(2)当P在AO上,
| 2t(6-t) |
| 2 |
解得:t1=2,t2=4.
∵t1=2,t2=4在0<t<6范围内,
∴t1=2,t2=4.
P在BO上,
| 2t(t-6) |
| 2 |
解得:t3=3+
| 17 |
| 17 |
∵t3=3+
| 17 |
∴t3=3+
| 17 |
(3)在Rt△BOQ中,由勾股定理,得
BQ2=4t2+36,
BP=12-t,BP2=144-24t+t2,
∵△PBQ是等腰三角形,
∴PB=BQ,
∴PB2=BQ2,
∴4t2+36=144-24t+t2,
解得:t1=-4+2
| 13 |
| 13 |
当PB=PQ时,BP2=144-24t+t2,PQ2=4t2+(12-t)2,
无解.
故答案为:-4+2
| 13 |
点评:本题考查了动点问题的运用,三角形的面积公式的运用,勾股定理的运用,一元二次方程的解法的运用,解答时运用直角三角形的性质及勾股定理是关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 如图,直线y=2x-4分别交x轴、y轴于B、A两点,交双曲线y=
如图,直线y=2x-4分别交x轴、y轴于B、A两点,交双曲线y= 如图,AB是半圆O的直径,弦AD,BC相交于点P,且CD,AB的长分别是一元二次方程x2-7x+12=0的两根,则cos∠DPB=
如图,AB是半圆O的直径,弦AD,BC相交于点P,且CD,AB的长分别是一元二次方程x2-7x+12=0的两根,则cos∠DPB= 如图,在菱形ABCD中 菱形ABCD的边长为2
如图,在菱形ABCD中 菱形ABCD的边长为2